Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) HS tự chứng minh
b) O nằm trên đường cao xuất phát từ đỉnh A của DABC
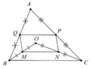

b) Giả sử MNPQ là hình chữ nhật
=> ^QMN=90do HAY QM vuong goc voi MN
Lai co MN//BC
=> BC vuong goc voi QM
Ma QM //AO
=> AO vuong goc voi BC
=> O thuoc duong cao ke tu A den BC
Goi giao diem cua AO VA BC LA H
Để SMNPQ=SABC
=> MQ.QP=(BC.AH)/2
Mà QP=BC/2
=> MQ=AH
Ma MQ=AH/2
=> AH=AO/2
Mà AO hay AH vuong goc voi BC
=> BC la trung truc cua AO .
Vay de tu giac MNPQ vua la HCN vua co dien h =tam giac ABC thi BC phai la trung truc cua AO
a,Do tia AO nằm giữa tia AB và tia AC(gt)
Gọi O là điểm nằm giữa đoạn thẳng BC
sao cho BO< OC
M,N,P,Q lần lượt là trung điểm của OB,OC,AC,AB (gt)
=>BM=MO;ON=NC;CP=PA;AQ=QB
Vậy ta có:PQ là đường trung bình của tam giác ABC nên PQ//=1/2 BC (1)
Tương tự:
PN là đường trung bình của tam giác ACO nên PN//=1/2 AO (2)
QM là đường trung bình của tam giác ABO nên QM//=1/2 AO (3)
Từ (2),(3) suy ra:
PN//=QM=1/2 OA ( t/c 2 đường thẳng//) (4)
Do đó PQ//=MN
=> Tứ giác MNPQ là hình bình hành
b,theo cmt : PN//=QM=1/2 OA
Mặt khác, AO là cạnh đối diện của 2 góc B và góc C
Từ đó=>góc B=góc C
=> tam giác ABC cân tại A
=>O là trung điểm của BC
=>AO _|_BC nên góc AOB=góc AOC=90°
=> 3 điểm B,O,C thẳng hàng (vì BOC=180°=góc AOB+góc AOC)
M,N là trung điểm của OB và OC(gt)
nên B,M,O,N,C thẳng hàng.
=>QM_|_BC và PN_|_BC
Hay góc QMN=góc PNM=1 vuông (5)
Theo (1) PQ//BC
=>PQ_|_QM ; PQ_|_PN
Hay góc MQP=góc NPQ=1 vuông (6)
Từ (5),(6) suy ra:
Tứ giác MNPQ là hình chữ nhật (đpcm)

Lỗi nên không vẽ được hình nha bạn !!!
Bài giải
Gọi E,F , R , S theo thứ tự là trung điểm của đường cao AH ,cạnh BC ,MQ ,NP.Gọi O là trung điểm của RS .Dùng bổ đề hình thang chứng minh B,R,E thẳng hàng ,C,S,E thẳng hàng ,E , O ,F thẳng hàng .Điểm O chuyển động trên đoạn thẳng EF, trừ E và F .

o giả thiết cho IJ không song song với CDvà chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K=IJ∩CDK=IJ∩CD.
Ta có : M là điểm chung thứ nhất của (ACD) và (IJM);
{K∈IJIJ⊂(MIJ)⇒K∈(MIJ){K∈IJIJ⊂(MIJ)⇒K∈(MIJ) và {K∈CDCD⊂(ACD)⇒K∈(ACD){K∈CDCD⊂(ACD)⇒K∈(ACD)
Vậy (MIJ)∩(ACD)=MK(MIJ)∩(ACD)=MK
Quảng cáo
b) Với L=JN∩ABL=JN∩AB ta có:
{L∈JNJN⊂(MNJ)⇒L∈(MNJ){L∈JNJN⊂(MNJ)⇒L∈(MNJ)
{L∈ABAB⊂(ABC)⇒L∈(ABC){L∈ABAB⊂(ABC)⇒L∈(ABC)
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P=JL∩AD,Q=PM∩ACP=JL∩AD,Q=PM∩AC
Ta có:
{Q∈PMPM⊂(MNP)⇒Q∈(MNJ){Q∈PMPM⊂(MNP)⇒Q∈(MNJ)
Và {Q∈ACAC⊂(ABC)⇒Q∈(ABC){Q∈ACAC⊂(ABC)⇒Q∈(ABC)
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ=(ABC)∩(MNJ)LQ=(ABC)∩(MNJ).

Để cho 3 cái đều có diện tích là \(\frac{1}{3}ABC\) thì :
Trước tiên ta nối AD. Ta được SABC=SADC=1/2 SABC
Để vẽ được BED bằng 1/3 SABC thì ta vẽ SBED= \(\frac{1}{3}:\frac{1}{2}\left(S_{ABD}\right)=\frac{2}{3}S_{ABD}\) hay còn nói : BE=2/3 BA
Tương tự với tam giác GDC
Phần còn lại là tứ giác và cũng bằng 2 tam giác kia