Cho hàm số bậc nhất y=x+2 (d) và y=-2x+8 (d')
a) Vẽ đồ thị hàm số trên cùng hệ trục tọa độ
b) Hai đường thẳng trên cắt nhau tại A và cắt trục Ox lần lượt tại B và C. Tính diện tích tam giác ABC.
help me
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 11 2021
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
30 tháng 1 2023
b: Tọa độ giao điểm là:
2x-1=x+2 và y=x+2
=>3x=3 và y=x+2
=>x=1 và y=3
a: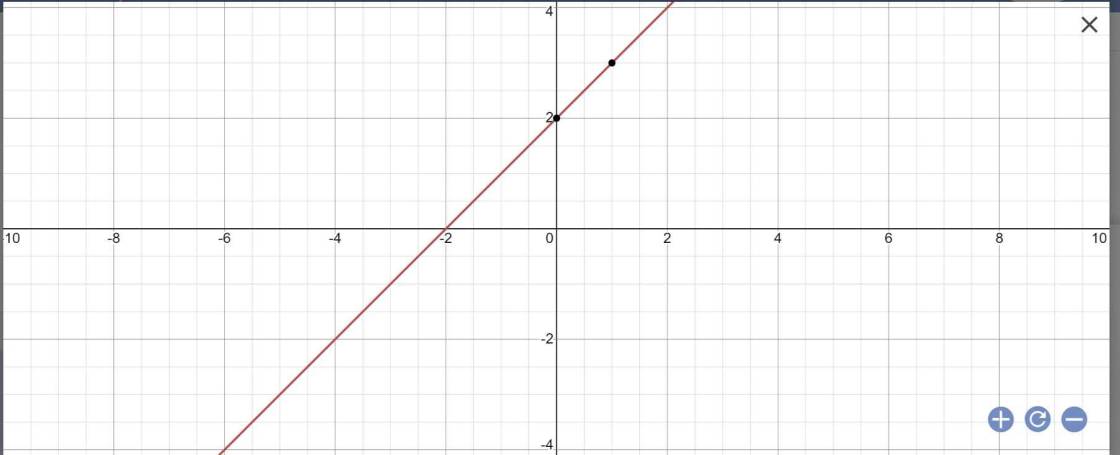 
5 tháng 3 2022
a: Để hai đường song song thì m+2=4
hay m=2
b: Tọa độ giao điểm của y=-3x+4 và y=2x-1 là:
\(\left\{{}\begin{matrix}-3x+4=2x-1\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Thay x=1 và y=1 vào (d), ta được:
m+2+m-3=1
=>2m-1=1
hay m=1
CM
30 tháng 8 2017
Đáp án B
• Ta thấy d: y = (m + 2)x - m có a = m + 2; b = -m và d': y = -2x - 2m + 1 có
• Để y = (m + 2)x - m là hàm số bậc nhất thì m + 2 ≠ 0 ⇔ m ≠ -2
• Để d // d' ⇔ a = a'; b ≠ b'
a = a' ⇔ m + 2 = -2 ⇔ m = -4
b ≠ b' ⇔ -m ≠ -2m + 1 ⇔ m ≠ 1
Vì m = -4 thỏa mãn m ≠ -2; m ≠ 1 nên giá trị m cần tìm là m = -4
Vậy m = -4
CM
16 tháng 8 2017
Ta thấy d : y = ( m + 2 ) x – m c ó a = m + 2 ≠ 0 ⇔ m ≠ 2 v à d ’ : y = − 2 x − 2 m + 1 c ó a ’ = − 2 ≠ 0 .
Để d // d’ ⇔ a = a ' b ≠ b ' ⇔ m + 2 = − 2 − m ≠ − 2 m + 1 ⇔ m = − 4 m ≠ 1 ⇔ m = − 4 ( T M )
Đáp án cần chọn là: B
CM
6 tháng 10 2017
Đáp án B
• Ta thấy d: y = (m + 2)x - m có a = m + 2; b = -m và d': y = -2x - 2m + 1 có
• Để y = (m + 2)x - m là hàm số bậc nhất thì m + 2 ≠ 0 ⇔ m ≠ -2
• Để d // d' ⇔ a = a'; b ≠ b'
a = a' ⇔ m + 2 = -2 ⇔ m = -4
b ≠ b' ⇔ -m ≠ -2m + 1 ⇔ m ≠ 1
Vì m = -4 thỏa mãn m ≠ -2; m ≠ 1 nên giá trị m cần tìm là m = -4
Vậy m = -4
CM
26 tháng 10 2017
Đáp án C
• Ta thấy d: y = (m + 2)x - m có a = m + 2 và d': y = -2x - 2m + 1 có a' = -2
• Để y = (m + 2)x - m là hàm số bậc nhất thì m + 2 ≠ 0 ⇔ m ≠ -2
• Để d cắt d' ⇔ a ≠ a' ⇔ m + 2 ≠ -2 ⇔ m ≠ -4
Vậy m ≠ -2; m ≠ -4
Lời giải:
a. Bạn tự vẽ hình
b. PT hoành độ giao điểm của $(d), (d')$:
$x+2=-2x+8\Leftrightaarrow 3x=6\Leftrightarrow x=2$
$y=x+2=2+2=4$
Vậy $A$ có tọa độ $(2,4)$
$B\in Ox$ nên $y_B=0$
$B\in (d)$ nên $y_B=x_B+2\Rightarrow x_B=y_B-2=0-2=-2$
Vậy $B(-2,0)$
$C\in Ox$ nên $y_C=0$
$C\in (d')$ nên $y_C=-2x_C+8\Rightarrow x_C=\frac{y_C-8}{-2}=\frac{-8}{-2}=4$
Vậy $C(4,0)$
Diện tích tam giác $ABC$:
$S_{ABC}=\frac{d(A,BC).BC}{2}=\frac{d(A,Ox).BC}{2}=\frac{|y_A|(|x_B|+|x_C|)}{2}=\frac{4(2+4)}{2}=12$ (đvdt)
Dài quá bạn ơi