cho các số x,y,z khác 0 thỏa mãn y+z+1/x=x+z+2/y=y+x-3/z=1/x+y+z tính giá trị biểu thứcM=(x+y+z)^2
nhanh vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2018
\(\left(x-1\right)^2\ge0\Rightarrow x^2-2x+1\ge0\Rightarrow x^2+1\ge2x\)
\(\left(y-2\right)^2\ge0\Rightarrow y^2-4y+4\ge0\Rightarrow y^2+4\ge4y\)
\(\left(z-3\right)^2\ge0\Rightarrow z^2-6z+9\ge0\Rightarrow z^2+9\ge6z\)
Do đó: \(\left(x^2+1\right)\left(y^2+4\right)\left(z^2+9\right)\ge2x.4y.6z=48xyz\)
Dấu "=" xảy ra khI: \(\hept{\begin{cases}x-1=0\\y-2=0\\z-3=0\end{cases}\Rightarrow\hept{\begin{cases}x=1\\y=2\\z=3\end{cases}}}\)
Vậy \(C=\frac{1^3+2^3+3^3}{\left(1+2+3\right)^3}=\frac{6^2}{6^3}=\frac{1}{6}\)
Chúc bạn học tốt.
GH
19 tháng 6 2023
\(\dfrac{y+z-x}{x}=\dfrac{z+x-y}{y}=\dfrac{x+y-z}{z}\\ \Rightarrow\dfrac{y+z-x}{x}+2=\dfrac{z+x-y}{y}+2=\dfrac{x+y-z}{z}+2\\ \Rightarrow\dfrac{x+y+z}{x}=\dfrac{x+y+z}{y}=\dfrac{x+y+z}{z}\\ \Rightarrow x=y=z\\ \Rightarrow A=\left(1+1\right).\left(1+1\right).\left(1+1\right)=8\)
XO
30 tháng 10 2019
Ta có : \(B=\frac{x+y}{y}.\frac{z+y}{z}=\frac{x+z}{x}=\frac{\left(x+y\right)\left(z+y\right)\left(x+z\right)}{xyz}\)
Từ \(\frac{y+z-x}{x}=\frac{z+x-y}{y}=\frac{x+y-z}{z}\)
\(\Rightarrow\frac{y+z-x}{x}+2=\frac{z+x-y}{y}+2=\frac{x+y-z}{z}+2\)
\(\Rightarrow\frac{x+y+z}{x}=\frac{x+y+z}{y}=\frac{x+y+z}{z}\)
Nếu x + y + z = 0
=> x + y = - z
=> z + y = - x
=> z + x = - y
Khi đó : B = \(\frac{\left(-x\right)\left(-y\right)\left(-z\right)}{xyz}=-\frac{xyz}{xyz}=-1\)
Nếu x + y + z \(\ne\)0
=> \(\frac{1}{x}=\frac{1}{y}=\frac{1}{z}\Rightarrow x=y=z\)
Khi đó \(B=\frac{\left(x+y\right)^3}{x^3}=\frac{\left(2x\right)^3}{x^3}=\frac{2^3.x^3}{x^3}=8\)
Vậy nếu x + y + z = 0 B = - 1
nếu x + y + z \(\ne\)0 thì B = 8
7 tháng 11 2018
thay z = -(x+y) , y = -(z+x),... vao
=> Duoc bieu thuc trong do co 1/xy + 1/yz + 1/zx = (x+y+z)/xyz = 0
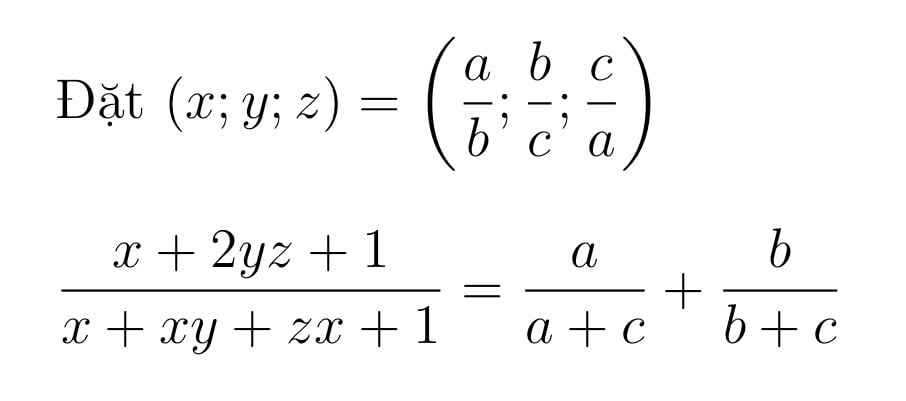
Lời giải:
Áp dụng TCDTSBN:
$\frac{1}{x+y+z}=\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{y+x-3}{z}=\frac{y+z+1+x+z+2+y+x-3}{x+y+z}=\frac{2(x+y+z)}{x+y+z}=2$
$\Rightarrow x+y+z=0,5$
Có:
$\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{y+x-3}{z}=2$
$\Rightarrow \frac{y+z+1}{x}+1=\frac{x+z+2}{y}+1=\frac{y+x-3}{z}+1=3$
$\Rightarrow \frac{x+y+z+1}{x}=\frac{x+y+z+2}{y}=\frac{x+y+z-3}{z}=3$
$\Rightarrow \frac{1,5}{x}=\frac{2,5}{y}=\frac{-2,5}{z}=3$
$\Rightarrow x=0,5; y=\frac{5}{6}; z=\frac{-5}{6}$