Cho hàm số \(y=2x+6\) (d1) và \(y=-\dfrac{1}{2}x+3\) (d2)
a) Vẽ đồ thị hàm số trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm C của (d1) và (d2) bằng phép tính.
c) Gọi A, B thứ tự là giao điểm của (d1) và (d2) với trục Ox. Tính SABC .
d) Tính khoảng cách từ M(0 ; -3) đễn đường thẳng (d2).

a: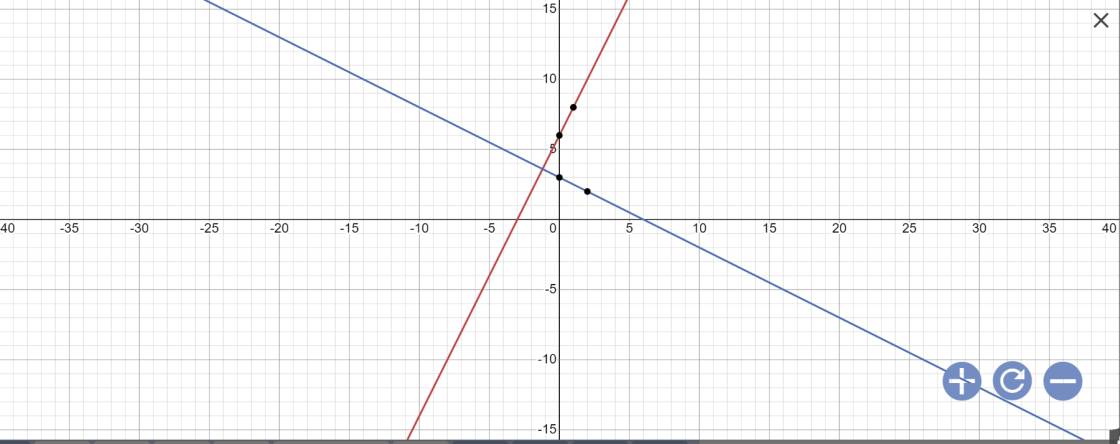
b: Phương trình hoành độ giao điểm là:
\(2x+6=-\dfrac{1}{2}x+3\)
=>\(\dfrac{5}{2}x=-3\)
=>\(x=-3:\dfrac{5}{2}=-\dfrac{6}{5}\)=-1,2
Thay x=-1,2 vào y=2x+6, ta được:
\(y=2\cdot\left(-1,2\right)+6=3,6\)
vậy: C(-1,2;3,6)
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\2x+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=0\end{matrix}\right.\)
vậy: A(-3;0); B(6;0); C(-1,2;3,6)
\(AB=\sqrt{\left(6+3\right)^2+\left(0-0\right)^2}=9\)
\(AC=\sqrt{\left(-1,2+3\right)^2+\left(3,6-0\right)^2}=\dfrac{9\sqrt{5}}{5}\)
\(BC=\sqrt{\left(-1,2-6\right)^2+\left(3,6-0\right)^2}=\dfrac{18\sqrt{5}}{5}\)
Vì \(AC^2+BC^2=AB^2\)
nên ΔABC vuông tại C
=>\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{9}{\sqrt{5}}\cdot\dfrac{18}{\sqrt{5}}=\dfrac{81}{5}\)
d: (d2): y=-1/2x+3
=>\(-\dfrac{1}{2}x-y+3=0\)
\(d\left(M;\left(d2\right)\right)=\dfrac{\left|0\cdot\left(-\dfrac{1}{2}\right)+\left(-3\right)\cdot\left(-1\right)+3\right|}{\sqrt{\left(-\dfrac{1}{2}\right)^2+\left(-1\right)^2}}=6:\dfrac{\sqrt{5}}{2}=\dfrac{12}{\sqrt{5}}\)