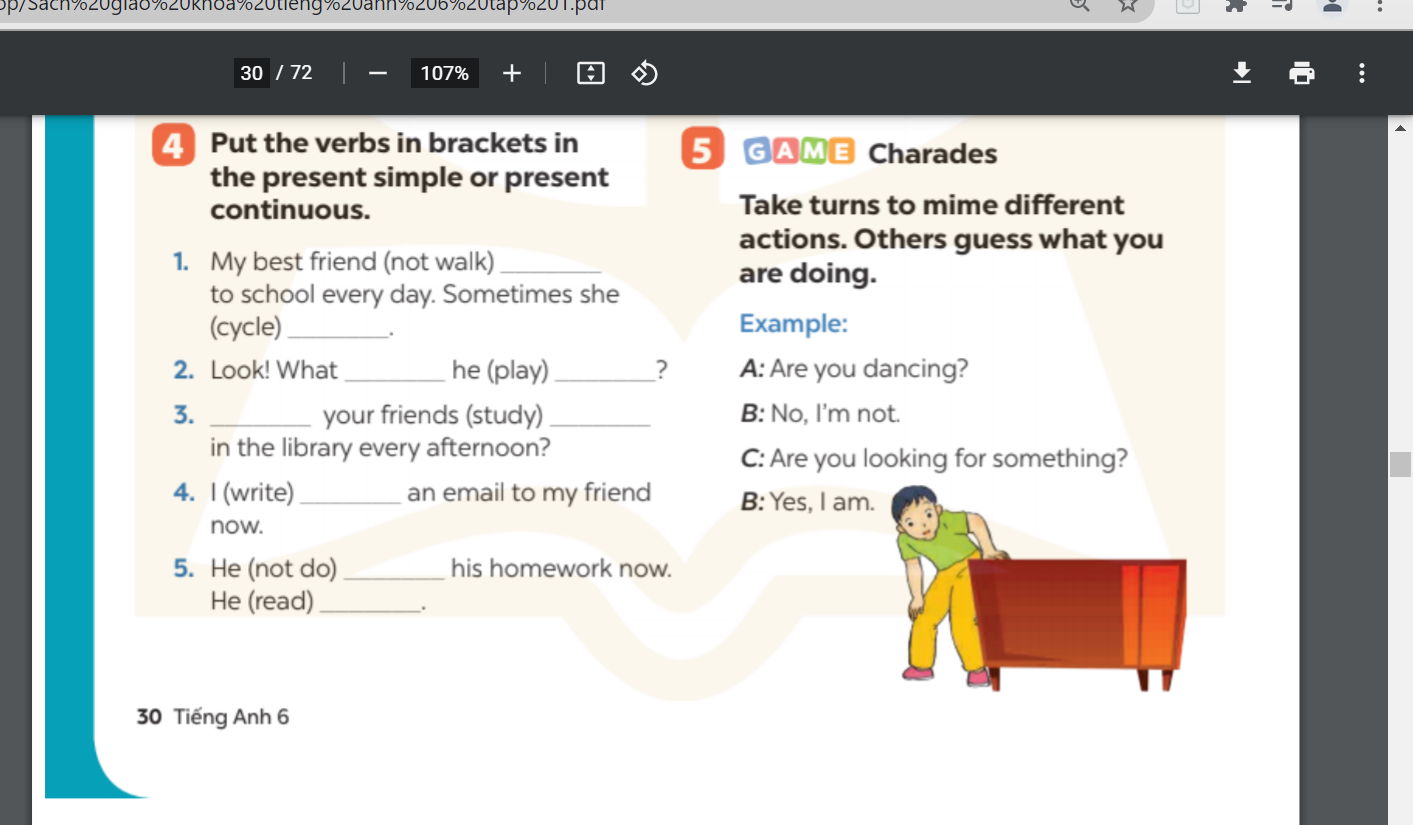
Mong các bạn giúp mình ạ.Vẽ hình nữa ạ.Cảm ơn!
Mong các bạn giúp mình ạ.Vẽ hình nữa ạ.Cảm ơn!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


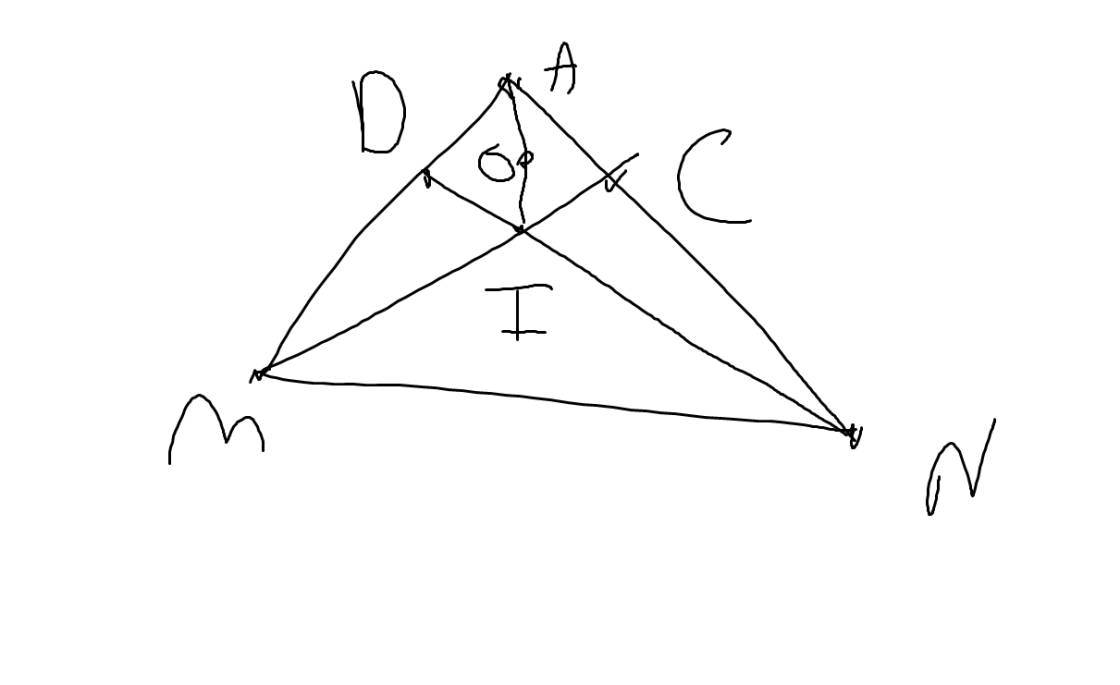
a: Sửa đề: Hai đường cao MC và ND cắt nhau tại I
Xét tứ giác MDCN có \(\widehat{MDN}=\widehat{MCN}=90^0\)
nên MDCN là tứ giác nội tiếp
=>M,D,C,N cùng thuộc một đường tròn
b: Xét tứ giác ADIC có
\(\widehat{ADI}+\widehat{ACI}=90^0+90^0=180^0\)
=>ADIC là tứ giác nội tiếp đường tròn đường kính AI
=>A,D,I,C cùng thuộc đường tròn đường kính AI
Tâm O là trung điểm của AI

tham khảo;-;
* Diễn biến: từ ngày 13-3-1954 đến hết ngày 7-5-1954, chia làm 3 đợt:
- Đợt 1 (từ 13-3 đến 17-03-1954): ta tiến công tiêu diệt cứ điểm Him Lam và toàn bộ phân khu Bắc.
- Đợt 2 (từ 30-3 đến 26-04-1954):
+ Quân ta đồng loạt tiến công các cứ điểm phía Đông phân khu trung tâm Mường Thanh.
+ Cuộc chiến đấu diễn ra vô cùng ác liệt, nhất là đồn A1, C1.
+ Ta bao vây, chia cắt, khống chế con đường tiếp tế bằng hàng không của địch.
- Đợt 3 (từ 1-5 đến ngày 7-5-1954):
+ Quân ta đồng loạt tiến công tiêu diệt phân khu trung tâm Mường Thanh và phân khu Nam.
+ Chiều ngày 7-5-1954, tướng Đờ Ca-xtơ-ri cùng toàn bộ Ban tham mưu của địch đầu hàng.
+ Chiến dịch Điện Biên Phủ giành thắng lợi.
REFER
* Diễn biến: từ ngày 13-3-1954 đến hết ngày 7-5-1954, chia làm 3 đợt:
- Đợt 1 (từ 13-3 đến 17-03-1954): ta tiến công tiêu diệt cứ điểm Him Lam và toàn bộ phân khu Bắc.
- Đợt 2 (từ 30-3 đến 26-04-1954):
+ Quân ta đồng loạt tiến công các cứ điểm phía Đông phân khu trung tâm Mường Thanh.
+ Cuộc chiến đấu diễn ra vô cùng ác liệt, nhất là đồn A1, C1.
+ Ta bao vây, chia cắt, khống chế con đường tiếp tế bằng hàng không của địch.
- Đợt 3 (từ 1-5 đến ngày 7-5-1954):
+ Quân ta đồng loạt tiến công tiêu diệt phân khu trung tâm Mường Thanh và phân khu Nam.
+ Chiều ngày 7-5-1954, tướng Đờ Ca-xtơ-ri cùng toàn bộ Ban tham mưu của địch đầu hàng.
+ Chiến dịch Điện Biên Phủ giành thắng lợi.

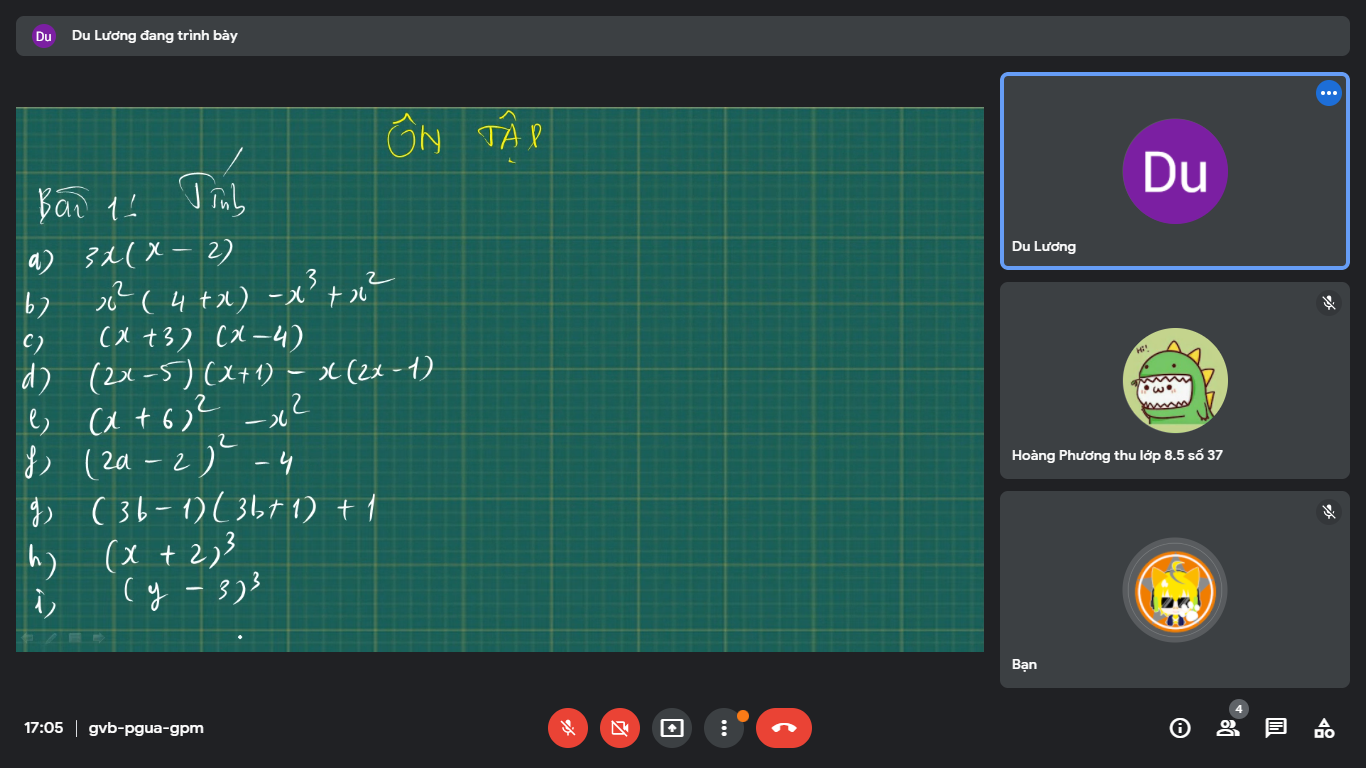
\(a,=3x^2-6x\\ b,=4x^2+x^3-x^3+x^2=5x^2\\ c,=x^2-4x+3x-12=x^2-x-12\\ d,=2x^2+2x-5x-5-2x^2+x=-2x-5\\ e,=x^2+12x+36-x^2=12x+36\\ f,=4a^2-8a+4-4=4a^2+8a\\ g,=9b^2-1+1=9b^2\\ h,=x^3+6x^2+12x+8\\ i,=y^3-9y^2+27y-27\)

Câu 1.
\(M=\left(-\dfrac{2a^3b^2}{3}xy^2z\right)^3.\left(-\dfrac{3}{4}ab^{-3}x^2yz^2\right)^2.\left(-xy^2z^2\right)^2\)
\(=\left(-\dfrac{8}{27}a^9b^6x^3y^6z^3\right).\left(\dfrac{9}{16}a^2b^{-6}x^4y^2z^4\right).\left(x^2y^4z^4\right)\)
\(=-\dfrac{8}{27}.\dfrac{9}{16}.a^{11}x^9y^{12}z^{11}\)
\(=-\dfrac{1}{6}a^{11}x^9y^{12}z^{11}\)
Hệ số: \(-\dfrac{1}{6}\)
Bậc: \(43\)
Câu 2.
a) \(A\left(x\right)=\dfrac{1}{2}x^5+\dfrac{3}{4}x-12x^4-1\dfrac{2}{3}x^3+5+x^2+\dfrac{5}{3}x^3-\dfrac{11}{4}x+1\dfrac{1}{2}x^5+4x\)
\(=\left(\dfrac{1}{2}x^5+\dfrac{3}{2}x^5\right)+\left(-12x^4\right)+\left(-\dfrac{5}{3}x^3+\dfrac{5}{3}x^3\right)+x^2+\left(\dfrac{3}{4}x-\dfrac{11}{4}x+4x\right)+5\)
\(=2x^5-12x^4+x^2+2x+5\)
\(B\left(x\right)=-2x^5+\dfrac{3}{7}x+12x^4-\dfrac{7}{3}x^3-3-6x^2+\dfrac{13}{3}x^3+3\dfrac{4}{7}x\)
\(=\left(-2x^5\right)+12x^4+\left(-\dfrac{7}{3}x^3+\dfrac{13}{3}x^3\right)-6x^2+\left(\dfrac{3}{7}x+\dfrac{25}{7}x\right)-3\)
\(=-2x^5+12x^4+2x^3-6x^2+4x-3\)
b) \(C\left(x\right)=A\left(x\right)+B\left(x\right)=\left(2x^5-12x^4+x^2+2x+5\right)+\left(-2x^5+12x^4+2x^3-6x^2+4x-3\right)\)
\(=\left(2x^5-2x^5\right)+\left(-12x^4+12x^4\right)+2x^3+\left(x^2-6x^2\right)+\left(2x+4x\right)+\left(5-3\right)\)
\(=2x^3-5x^2+6x+2\)
\(D\left(x\right)=A\left(x\right)-B\left(x\right)=\left(2x^5-12x^4+x^2+2x+5\right)-\left(-2x^5+12x^4+2x^3-6x^2+4x-3\right)\)
\(=\left(2x^5+2x^5\right)+\left(-12x^4-12x^4\right)-2x^3+\left(x^2+6x^2\right)+\left(2x-4x\right)+\left(5+3\right)\)
\(=4x^5-24x^4-2x^3+7x^2-2x+8\)
c) \(2x^3-5x^2+6x+2-2x^3+5x^2=-4\)
\(\Rightarrow\left(2x^3-2x^3\right)+\left(-5x^2+5x^2\right)+6x+2\)
\(\Rightarrow6x+2=-4\)
\(\Rightarrow6x=-6\)
\(\Rightarrow x=-1\)
Câu 3.
1) \(M-3xy^2+2xy-x^3+2x^2y=2xy-3x^3+3x^2y-xy^2\)
\(\Rightarrow M=\left(3xy^2+2xy-x^3+2x^2y\right)+\left(2xy-3x^3+3x^2y-xy^2\right)\)
\(=\left(3xy^2-xy^2\right)+\left(2xy+2xy\right)+\left(-x^3-3x^3\right)+\left(2x^2y+3x^2y\right)\)
\(=2xy^2+4xy-4x^3+5x^2y\)
2)
Để cho \(f\left(x\right)\) có nghiệm thì \(6-3x=0\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
Để cho \(g\left(x\right)\) có nghiệm thì \(x^2-1=0\)
\(\Rightarrow x^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

Ta có (x+1)^3 - (x-1)^3
=(x3+3x2+3x+1)-(x3-3x2+3x-1)
= x3 + 3x2 +3x +1 - x3 + 3x2 -3x + 1
=6x2 + 2
Vậy biểu thức này có phụ thuộc vào biến x (vì vẫn còn 6x2)
Chúc bạn học tốt!

* - Dao động của các sợi dây đàn mạnh, dây lệch nhiều khi phát ra tiếng to.
- Dao động của các sợi dây đàn yếu, dây lệch ít khi phát ra tiếng nhỏ.
* Muốn tiếng đàn phát ra to thì ta phải gảy mạnh vì biên độ dao động lớn, nên phát ra âm thanh to.

 mong mn giúp ạ.Cảm ơn mn.
mong mn giúp ạ.Cảm ơn mn.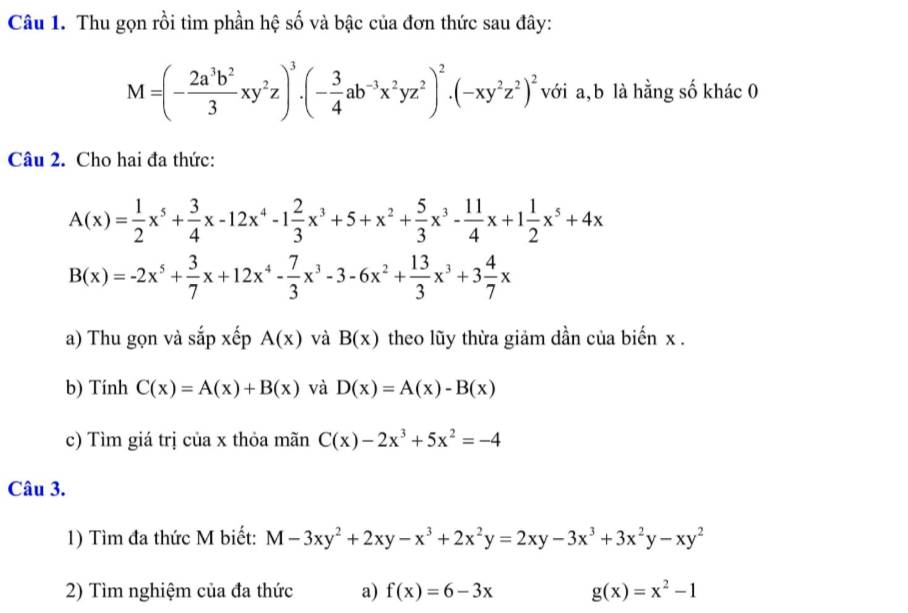
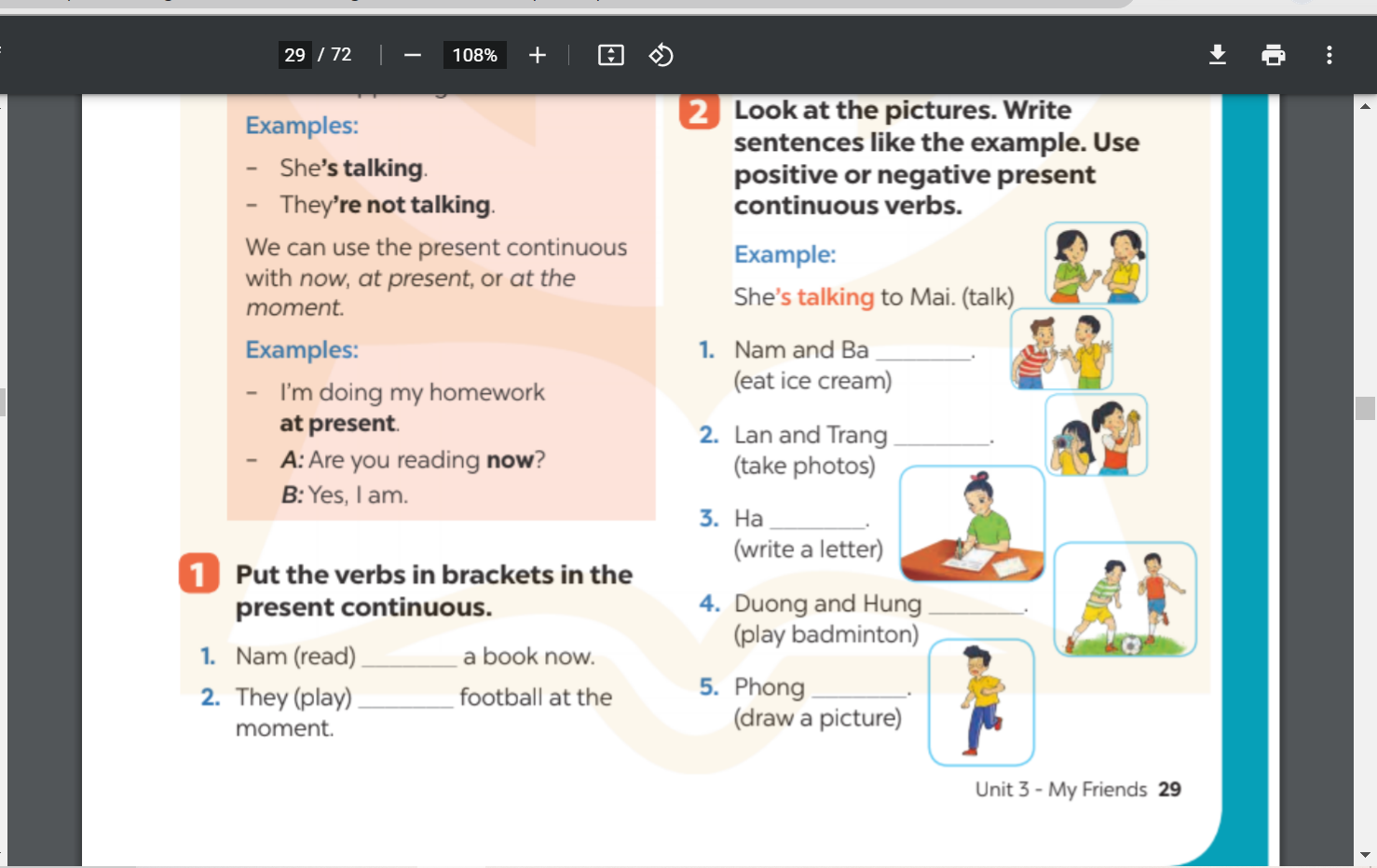 các bạn giúp mình bài 1, bài 2. trang 29 hình ở trên ạ
các bạn giúp mình bài 1, bài 2. trang 29 hình ở trên ạ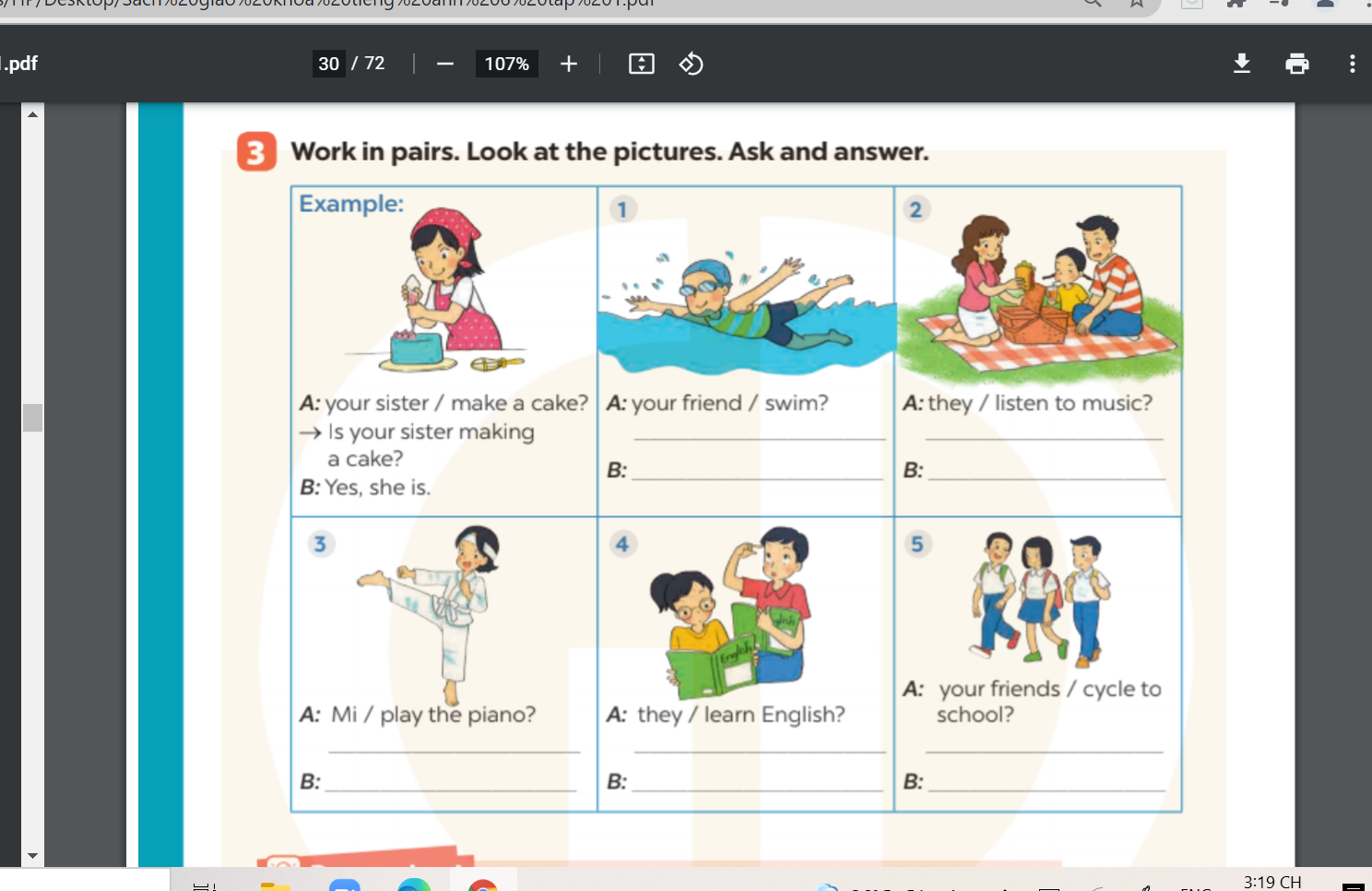 các bạn giúp mình bài 3 hình ở trên đó ạ
các bạn giúp mình bài 3 hình ở trên đó ạ