|
< |
|
< |
|
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giờ đây tôi đã là một cô học trò chững chạc, đã bước vào sân của ngôi trường THCS với nhiều điều mới mẻ. Nhưng, lm sao tôi có thể quên đc, những kí ức đẹp về mái trường tiểu học đầy ngây ngô thuở ấy. Đúng, trog đầu tôi thấp thoáng hiện về những hàng ghế đá xếp dọc theo hàng cây bàng to và rộng, mà ngày xưa chúng tôi hay ngồi trò chuyện tán gẫu với nhau, hay mấy chậu hoa lan trắng mà đích thân tôi trồng ở gần cửa sổ nhỏ. Tôi trông phía xa, có một hình ảnh hiện lên, đó là gương mặt của bạn bè, của thầy cô giáo cứ chốc chốc lại mỉm cười, hướng về tôi cùng ánh nhìn đầy niềm hy vọng. Tôi cảm giác như họ chờ đợi một điều gì đó ở cô học trò này, vì thế lúc nào tôi cũng tự nhủ mình phải cố gắng học tập để đền đáp công ơn của thầy cô giáo năm xưa và khiến cho bạn bè và cả bản thân tôi tự hào.
Từ đồng nghĩa: trông, nhìn.
Từ trái nghĩa: to, nhỏ.




-Vì bài dài quá nên mình nói tóm tắt:
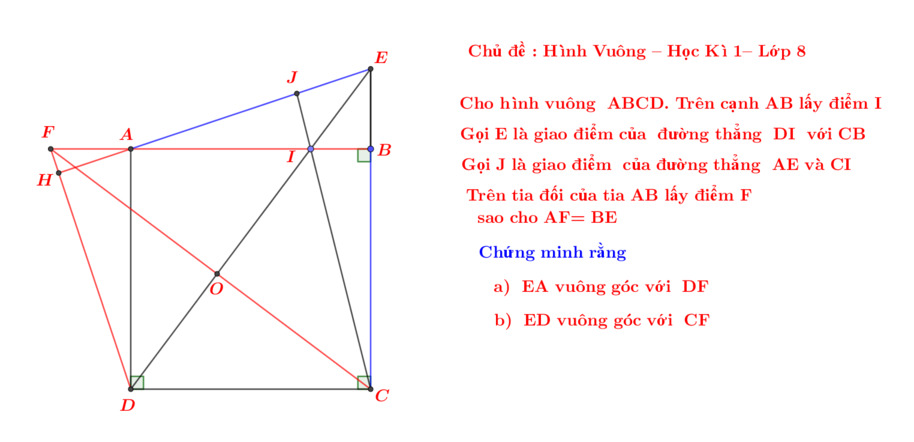
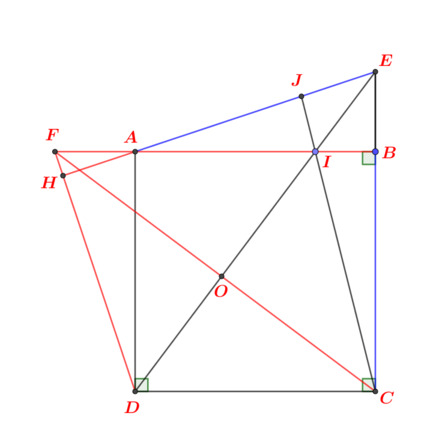
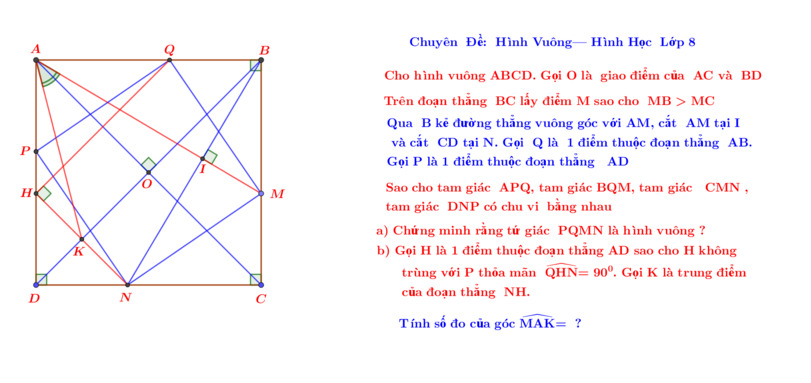
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......

Từ GT \(\Leftrightarrow a>0;bc>0\)
\(BĐT\Leftrightarrow\dfrac{a^2}{3}+\left(b+c\right)^2-3bc-a\left(b+c\right)\ge0\\ \Leftrightarrow\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\ge0\)
Vì \(a^3>36\) nên
\(\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\\ >\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}+\dfrac{1}{4}=\left(\dfrac{b+c}{a}-\dfrac{1}{2}\right)^2\ge0\)

Ta có : \(\dfrac{x}{15}\text{=}\dfrac{-1}{3}\)
\(\Rightarrow\dfrac{x}{15}\text{=}\dfrac{-5}{15}\)
\(\Rightarrow x\text{=}-5\)
\(\dfrac{x}{15}\)=\(\dfrac{-1}{3}\)
⇒x.3=15. -1
⇒x.3=-15
⇒x =-15 ; 3
⇒x =-5
Vậy x=-5



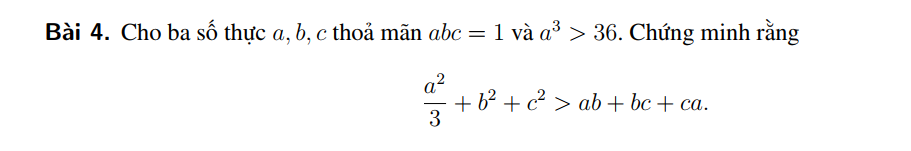
\(\dfrac{9}{14}\) < \(\dfrac{12}{◻}\) < \(\dfrac{9}{13}\)
\(\dfrac{9\times4}{14\times4}\) < \(\dfrac{12\times3}{◻\times3}\) < \(\dfrac{9\times4}{13\times4}\)
\(\dfrac{36}{56}\) < \(\dfrac{36}{◻\times3}\) < \(\dfrac{36}{52}\)
56 > \(◻\) \(\times\) 3 < 52
\(◻\) \(\times\) 3 = 54
\(◻\) = 54 : 3
\(◻\) = 18
Con cảm ơn cô Thương Hoài ạ