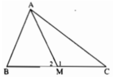
Cho tam giác ABC nhọn, M là điểm bất kỳ trên cạnh BC (M khác B;C). Từ M vẽ ME//AC với E thuộc AB, vẽ MF//AB với F thuộc AC. Chứng minh AE.EB + AF.FC > BM.MC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 3 2018
ΔABC có AB ≤ AC ⇒ ∠C ≤ ∠B.
ΔABM có ∠M1 là góc ngoài nên ∠M1 > ∠B
⇒ ∠M1 > ∠C
ΔAMC có ∠M1 > ∠C ⇒ AC > AM.
7 tháng 10 2021
a: Ta có: M và N đối xứng nhau qua AB
nên AB là đường trung trực của MN
Suy ra: AM=AN; BM=BN
Xét ΔABN và ΔABM có
AB chung
BN=BM
AN=AM
Do đó: ΔABN=ΔABM
CM
20 tháng 5 2019
Giả sử BM<MC khi đó: S(AMB)<S(AMC) Đặt I là trung điểm BC. Nối AM, AI. Qua I kẻ đường thẳng song song với AM và cắt AC tại N và AI giao với MN tại O. Đường thẳng MN chính là đường thẳng cần phải vẽ. Thật vây, tứ giác ANIM là hình thang nên S(AON)=S(MOI) Mặt khác: S(AIC)=1/2S(ABC)=S(AON)+S(CION)=S(MOI)+S(CION)=S(CMN)
CM
3 tháng 11 2017
Giả sử BM<MC khi đó: S(AMB)<S(AMC)
Đặt I là trung điểm BC. Nối AM, AI. Qua I kẻ đường thẳng song song với AM và cắt AC tại N và AI giao với MN tại O.
Đường thẳng MN chính là đường thẳng cần phải vẽ.
Thật vây, tứ giác ANIM là hình thang nên S(AON)=S(MOI)
Mặt khác:
S(AIC)=1/2S(ABC)=S(AON)+S(CION)=S(MOI)+S(CION)=S(CMN)
LM
31 tháng 8 2021
Bài 1 : a) M là trung điểm AB
N là trung điểm AC
suy ra : MN là Đường trung bình của tam giác ABC
suy ra : MN // BC ; MN = BC/2
b) Ta có : MN // BC và M là trung điểm AB
Mà AD cắt MN tại I nên từ đó suy ra : I là trung điểm của cạnh AD
em chỉ giải được bài 1 thôi nên thông cảm ạ