Mọi người giúp mik câu 6,7,8,9 nhé, đề bài mik để ở phần bình luận.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TS
2
30 tháng 10 2023
\(\widehat{x'MC}=\widehat{xMN}\)(hai góc đối đỉnh
mà \(\widehat{xMN}=60^0\)
nên \(\widehat{x'MC}=60^0\)
Mz là phân giác của \(\widehat{x'MC}\)
=>\(\widehat{x'Mz}=\widehat{CMz}=\dfrac{60^0}{2}=30^0\)
Mz//Nt
=>\(\widehat{zMC}=\widehat{tNM}\)(hai góc đồng vị)
=>\(\widehat{tNM}=30^0\)
Nt là phân giác của góc y'NM
=>\(\widehat{y'NM}=2\cdot\widehat{tMN}=60^0\)
TS
3
KV
1 tháng 11 2023
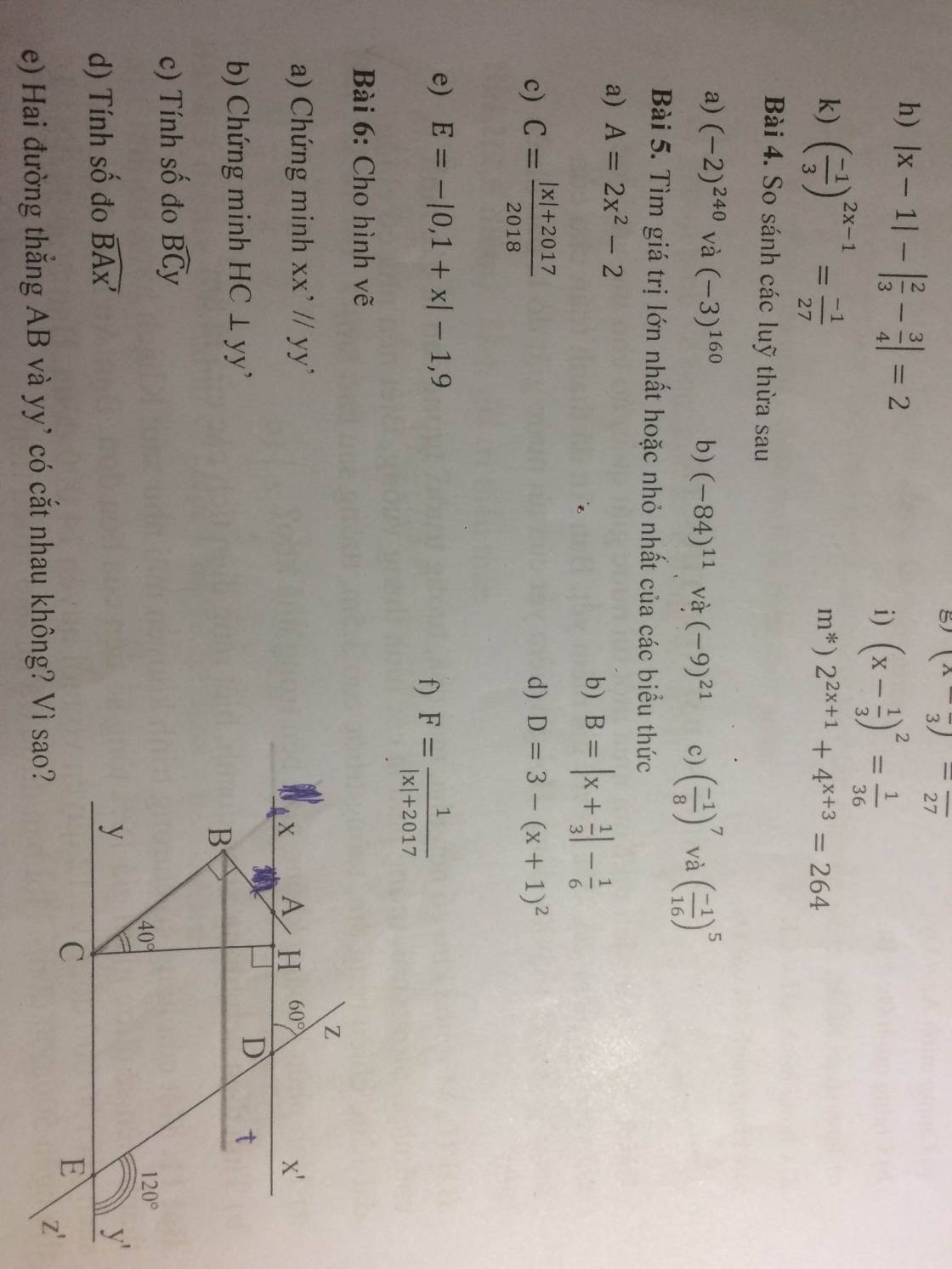
a) ∠CEz + ∠zEy' = 180⁰ (kề bù)
⇒ ∠CEz = 180⁰ - ∠zEy'
= 180⁰ - 120⁰
= 60⁰
⇒ ∠CEz = ∠xDz = 60⁰
Mà ∠CEz và ∠xDz là hai góc đồng vị
⇒ xx' // yy'
b) Do HC ⊥ xx' (gt)
xx' // yy' (cmt)
⇒ HC ⊥ yy'
c) Do HC ⊥ yy' (cmt)
⇒ ∠HCy = 90⁰
⇒ ∠BCy = ∠HCy - ∠BCH
= 90⁰ - 40⁰
= 50⁰
c) Vẽ tia Bt // xx'//yy'
⇒ ∠CBt = ∠BCy = 50⁰ (so le trong)
⇒ ∠ABt = ∠ABC - ∠CBt
= 90⁰ - 50⁰
= 40⁰
Do Bt // xx'
⇒ ∠xAB = ∠ABt = 40⁰ (so le trong)
Ta có:
∠BAx' + ∠xAB = 180⁰ (kề bù)
⇒ ∠BAx' = 180⁰ - ∠xAB
= 180⁰ - 40⁰
= 140⁰
e) Do AB cắt tia Bt tại B
Mà Bt // yy'
⇒ AB cắt yy'
TS
3
13 tháng 12 2023
bài 17:
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>DA=DE
Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
c: ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại I là trung điểm của AE
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
Do đó: ΔDAF=ΔDEC
=>\(\widehat{ADF}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{ADE}=180^0\)(hai góc kề bù)
nên \(\widehat{ADF}+\widehat{ADE}=180^0\)
=>D,E,F thẳng hàng
TS
2
5 tháng 11 2023
OM\(\perp\)AB
=>\(\widehat{MOA}=\widehat{MOB}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOE}< \widehat{AOM}\)
nên tia OE nằm giữa hai tia OA và OM
=>\(\widehat{AOE}+\widehat{MOE}=\widehat{AOM}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OB, ta có: \(\widehat{BOF}< \widehat{BOM}\)
nên tia OF nằm giữa hai tia OB và OM
=>\(\widehat{BOF}+\widehat{MOF}=\widehat{BOM}=90^0\)
=>\(\widehat{AOE}+\widehat{MOE}=\widehat{BOF}+\widehat{MOF}\)
mà \(\widehat{AOE}=\widehat{BOF}\)
nên \(\widehat{MOE}=\widehat{MOF}\)
=>OM là phân giác của \(\widehat{EOF}\)
TS
3
Bài 7:
a:
Ta có: ΔABC đều
=>AB=AC=BC và \(\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60^0\)
Xét ΔABC có \(\widehat{ACE}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACE}=\widehat{CAB}+\widehat{CBA}=120^0\)
Xét ΔACE có \(\widehat{ACE}>90^0\)
nên AE là cạnh lớn nhất trong ΔACE
=>AE>AC
=>AE>AB
b: Xét ΔCAE có CA=CE(=BC)
nên ΔCAE cân tại C
=>\(\widehat{CAE}=\dfrac{180^0-120^0}{2}=30^0\)
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
=>\(\widehat{HAC}=\dfrac{\widehat{BAC}}{2}=30^0\)
=>\(\widehat{HAC}=\widehat{CAE}\)
=>AC là phân giác của góc HAE
bài 9:
a: ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC
b: Xét ΔAHM vuông tại H có AM là cạnh huyền
nên AM là cạnh lớn nhất trong ΔAHM
=>AM>AH
Xét ΔAHM có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{AHM}+\widehat{HAM}=90^0+\widehat{HAM}\)
=>\(\widehat{AMB}>90^0\)
Xét ΔAMB có \(\widehat{AMB}>90^0\)
nên AB là cạnh lớn nhất trong ΔAMB
=>AB>AM
=>AB>AM>AH
=>AC>AM>AH