Cho tam giác ABC vuông tại A . Các tia phân giác của góc B và C cắt nhau ở I .Gọi D,E,F lần lượt là chân các đường vuông góc kẻ từ I đến AB,AC,BC
Chứng minh BD = ( BA + BC - AC ) : 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 4 2019
\(\Delta\)COE=\(\Delta\)COD(ch-gn)=>OE=OD
\(\Delta\)BOF=\(\Delta\)BOD(ch-gn)=>OD=OF
Suy ra: OD=OE=OF
b) mình nghĩ là ko bằng
CM
25 tháng 6 2018
Vì I là giao điểm các đường phân giác trong của B và C nên AI là tia phân giác của ∠A .
Suy ra: ID = IE (tính chất tia phân giác) (1)
Vì ΔADI vuông tại D có AI là tia phân giác góc A nên: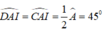 
Do đó: ΔADI vuông cân tại D
Suy ra: ID = DA (2)
Vì ΔAEI vuông tại E có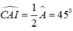 
nên ΔAEI vuông cân tại E
Suy ra: IE = AE (3)
Từ (1), (2) và (3) suy ra: AD = AE.
CM
16 tháng 7 2019
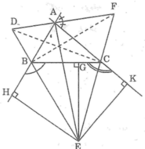
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
12 tháng 1 2017
bài toán này cũng dễ mà,nó ra là ... thôi bạn tự là đ
6 tháng 11 2017
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
G
18 tháng 11 2016
Hạ thêm IF vuông góc với BC
Vì BI là phân giác góc B nên IE = IF
Vì CI là phân giác góc B nên ID = IF
=> IE = ID (cùng = IF)
Tứ giác ADIE là hình chữ nhật (vì có 3 góc vuông) và có 2 cạnh liên tiếp bằng nhau (IE=ID) nên nó là hình vuông
=> AD = AE
16 tháng 2 2019
1. Mật khẩu vào cửa
Anh Tèo lần đầu đi Mỹ muốn ghé thăm một quán bar "xịn sò". Tuy nhiên, quán này lại chỉ cho phép những hội viên có mật khẩu vào mà thôi.
Cực chẳng đã, anh chàng phải đứng ngoài hóng xem mật khẩu từ khách đến trước là gì. Và đoạn hội thoại Tèo nghe được như sau.
Khi một cô gái đến gần, bảo vệ nói: "Twelve (12)", cô đáp "Six (6)" và được cho vào.
Một anh chàng khác đến, bảo vệ nói: "Six (6)", anh đáp "Three (3)" và được cho vào.
Sở hữu vốn tiếng Anh khá chuẩn, Tèo tự tin bước vào. Bảo vệ nói "Ten (10)", Tèo đáp: "Five (5)" rất dứt khoát, nhưng vẫn không được vào.
Vậy mật khẩu ở đây là gì?
2. Vụ cướp kỳ lạ
Một người đàn ông với mặt mày xước xát chạy đến đồn cảnh sát và thông báo rằng mình vừa bị cướp. Câu chuyện được thuật lại như sau: "Tôi đến ngân hàng, cầm theo vali chứa $100.000. Nhưng một kẻ mặc áo đen, quần đen, đeo mặt nạ và găng tay đen xuất hiện và tấn công. Hắn giật lấy vali rồi chạy mất tiêu."
Khi được hỏi về vết xước, ông ta đáp: "Kẻ đó tấn công tôi. Tay hắn có đeo một chiếc nhẫn bạc, bên tay trái, nó gây ra vết xước."
Cảnh sát kết luận người này nói dối. Hỏi tại sao?
3. Chuyến đò nguy hiểm
Jack nuôi 1 con sư tử, 1 con cừu, và mang theo một bao cỏ. Anh muốn qua sông, nhưng chỉ có một chiếc thuyền, và chiếc thuyền này cũng không thể chở quá 2 thứ cùng lúc.
Có nghĩa Jack phải chèo thuyền, và mỗi lần chỉ được mang theo một trong ba thứ anh có. Nhưng đồng thời, anh cũng phải đảm bảo rằng cừu không được ở một mình với bao cỏ, cũng như sư tử không được ở cùng cừu.
Giải pháp cho anh là gì?
4. Cửa an toàn
Một anh chàng vô tình bị kẻ xấu nhốt, nhưng chúng khá vui tính khi chỉ cho anh 4 cánh cửa. Cả 4 đều có thể thoát, nhưng sẽ phải trải qua thử thách bên trong.
Cánh cửa đầu tiên sẽ khiến anh rơi vào bể đầy cá mập trắng. Cửa 2 đằng sau chứa đầy nước, sẽ khiến cả căn phòng ngập nhanh chóng. Cửa 3 là một căn phòng ngập khí độc. Và cửa 4, anh sẽ phải đối mặt với một kẻ giết người hàng loạt bệnh hoạn và đáng sợ bậc nhất, đã giết hơn 100 người từ năm 1918.
Hỏi: Anh chàng phải chọn cửa nào để sống.
5. Thần bài
Bạn bị bịt mắt, và được đưa cho một bộ 52 lá bài. Vấn đề là trong bộ bài có 13 lá đang lật ngửa, và nhiệm vụ của bạn là tách cỗ bài ra làm 2, sao cho mỗi bên có số lá bài ngửa bằng nhau.
Bạn sẽ làm gì?
6. Vật thể lạ
Hình nào là khác biệt nhất so với các hình còn lại? (Câu đố này từng làm khó cả sinh viên đại học Harvard đấy).
21 tháng 12 2022
a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD
21 tháng 12 2022
a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD
Do I là giao điểm 2 đường phân giác góc B và C nên AI cũng là phân giác góc A
ID vuông góc AB nên tam giác BID vuông tại D
IF vuông góc AC nên tam giác BIF vuông tại F
Xét hai tam giác vuông BID và BIF có:
\(\left\{{}\begin{matrix}BI\text{ là cạnh chung}\\\widehat{IBD}=\widehat{IBF}\left(\text{do IB là phân giác}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta_VBID=\Delta_VBIF\left(ch-gn\right)\)
\(\Rightarrow BD=BF\)
Chứng minh tương tự, ta cũng có: \(AD=AE\) ; \(CE=CF\)
Từ đó ta có:
\(\left(BA+BC-AC\right):2=\left(BD+AD+BF+CF-AE-CE\right):2\)
\(=\left(BD+BF\right):2=2BD:2=BD\) (đpcm)