Chi tiết em nới học nên làm chi tiết nhất ạ 
đề bài rút gọn phân thức
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HT
2
Những câu hỏi liên quan
2 tháng 12 2021
\(=\dfrac{-8xy\left(1-3x\right)^3:4x\left(1-3x\right)}{12x^3\left(1-3x\right):4x\left(1-3x\right)}=\dfrac{-2y\left(1-3x\right)^2}{3x^2}\)
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
Lời giải:
\(\frac{2x-2\sqrt{x}+2}{x-\sqrt{x}}=\frac{2(x-\sqrt{x})+2}{x-\sqrt{x}}=\frac{2(x-\sqrt{x})+2}{x-\sqrt{x}}=2+\frac{2}{x-\sqrt{x}}\)
4 tháng 9 2021
\(\dfrac{2x-2\sqrt{x}+2}{x\sqrt{x}+1}=\dfrac{2}{\sqrt{x}+1}\)
26 tháng 8 2023
5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)
0H
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 3 2022
ĐKXĐ: \(x>2\)
\(A=\dfrac{\sqrt{x-2-4\sqrt{x-2}+4}+\sqrt{x-2+4\sqrt{x-2}+4}}{\sqrt{\left(\dfrac{2}{x}-1\right)^2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{x-2}-2\right)^2}+\sqrt{\left(\sqrt{x-2}+2\right)^2}}{\left|\dfrac{2}{x}-1\right|}=\dfrac{\left|\sqrt{x-2}-2\right|+\left|\sqrt{x+2}+2\right|}{1-\dfrac{2}{x}}\)
- Với \(x\ge6\Rightarrow A=\dfrac{\sqrt{x-2}-2+\sqrt{x-2}+2}{\dfrac{x-2}{x}}=\dfrac{2x\sqrt{x-2}}{x-2}=\dfrac{2x}{\sqrt{x-2}}\)
- Với \(2< x< 6\Rightarrow A=\dfrac{2-\sqrt{x-2}+\sqrt{x-2}+2}{\dfrac{x-2}{x}}=\dfrac{4x}{x-2}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
ĐKXĐ: \(x\ge0;x\ne4\)
\(A=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{3\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}-\dfrac{12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
8 tháng 9 2021
\(e,\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\sqrt{5-2\sqrt{6}}\\ =\left(5+2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\left(5-2\sqrt{6}\right)^2\\ =\left(5-2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\\ =\left(\sqrt{3}-\sqrt{2}\right)^2\left(\sqrt{3}-\sqrt{2}\right)=\left(\sqrt{3}-\sqrt{2}\right)^3\)
\(f,\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\sqrt{8}\right)\cdot3\sqrt{6}\\ =36-36\sqrt{2}+30\sqrt{3}-3\sqrt{3}=36-36\sqrt{2}+27\sqrt{3}\)
\(g,\left(2+\sqrt{3}-\sqrt{2}\right)\left(2-\sqrt{3}-\sqrt{2}\right)\left(3+\sqrt{2}\right)\sqrt{3-2\sqrt{2}}\\ =\left[\left(2-\sqrt{2}\right)^2-\left(\sqrt{3}\right)^2\right]\left(3+\sqrt{2}\right)\sqrt{\left(\sqrt{2}-1\right)^2}\\ =\left(3-4\sqrt{2}\right)\left(3+\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =\left(1-9\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =10\sqrt{2}-37\)
\(h,A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\\ A^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\\ A^2=8+2\sqrt{6-2\sqrt{5}}\\ A^2=8+2\left(\sqrt{5}-1\right)\\ A^2=6+2\sqrt{5}\\ A=\sqrt{6+2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}=\sqrt{5}+1\)
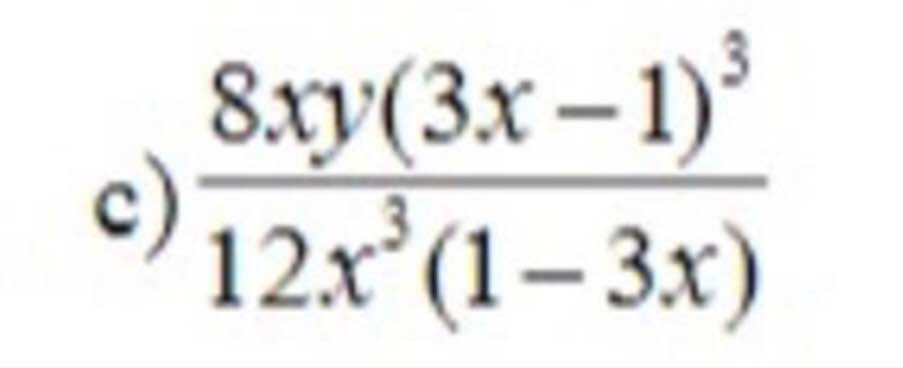
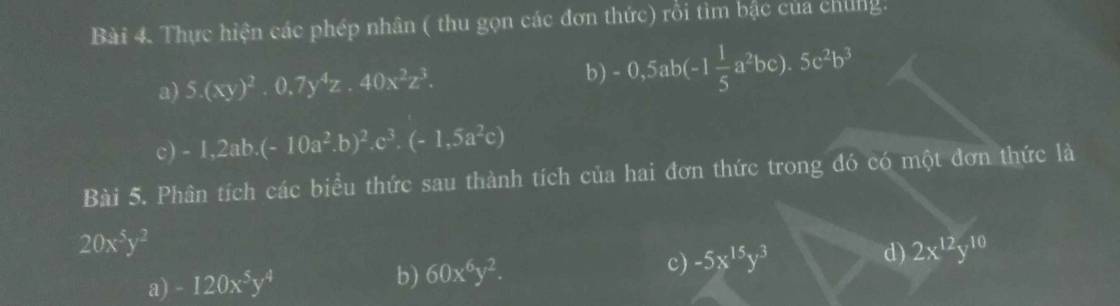
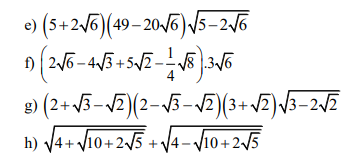
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)