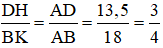Cho tam giác ABC và điểm D trên cạch AB sao cho AD=13,3cm,DB=4,5cm.Tính tỉ số các khoảng cách từ các điểm D và B trên cạch AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


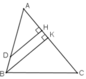
Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
⇒ AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Ta-lét ta có:
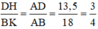
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4

Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
⇒ AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Ta-lét ta có:
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4
Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
⇒ AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Ta-lét ta có:
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4


Gọi DE và BF lần lượt là khoảng cách từ B và D đến cạnh AC.
Ta có DE // BF (cùng vuông góc với AC)
Áp dụng hệ quả của định lí ta – lét đối với ΔABF ta có:
Có AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
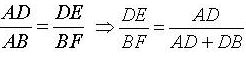

Vậy tỉ số khoảng cách từ điểm D và B đến AC bằng 0,75.
Gọi DH và BK lần lượt là khoảng cách từ B và D đến cạnh AC.
Ta có DH // BK (cùng vuông góc với AC)
=> DHBKDHBK = ADABADAB
Mà AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
Vậy DHBKDHBK = 13,51813,518 = 3434
Vậy tỉ số khoảng cách từ điểm D và B đến AC bằng 34

kẻ DH và BG vuông góc AC
=>DH//BG
Xét ΔABG có DH//BG
nên AD/DB=AH/HG=3
=>AH=3HG
=>DH/BG=3/4
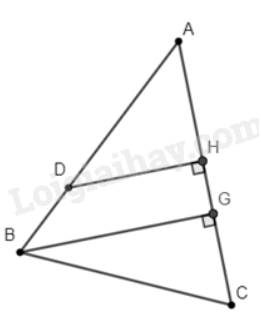
Gọi \(H;G\) lần lượt là hình chiếu vuông góc của \(D;B\)lên \(AC\).
Khi đó, khoảng cách từ \(D\) đến \(AC\) là \(DH\);khoảng cách từ \(B\) đến \(AC\) là \(BG\).
Ta có: \(AB = AD + BD = 13,5 + 4,5 = 18cm\)
Vì \(\left\{ \begin{array}{l}DH \bot AC\\BG \bot AC\end{array} \right. \Rightarrow DH//BG\)
Xét tam giác \(ABG\) có \(DH//BG\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{AB}} = \frac{{DH}}{{BG}} \Leftrightarrow \frac{{13,5}}{{18}} = \frac{{DH}}{{BG}} = \frac{3}{4}\)
Vậy tỉ số khoảng cách từ điểm \(D\) và \(B\) đến đoạn thẳng \(AC\) là \(\frac{3}{4}\).

Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK ( cùng vuông góc với AC ) nên áp dụng hệ quả định lí Ta-lét ta có :
\(\frac{DH}{BK}=\frac{AD}{AB}=\frac{13,5}{18}=\frac{3}{4}\)
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là \(\frac{3}{4}\)

Gọi DH và BK lần lượt là khoảng cách từ B và D đến cạnh AC.
Ta có DH // BK (cùng vuông góc với AC)
=> \(\frac{DH}{BK}\) = \(\frac{AD}{BC}\)
Mà AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
Vậy \(\frac{DH}{BK}\) = \(\frac{13,5}{18}=\frac{3}{4}\)
Vậy tỉ số khoảng cách từ điểm D và B đến AC bằng

Bài 1:
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó:ΔABE=ΔACD
Suy ra: BE=CD
b: Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{KDB}=\widehat{KEC}\)
Xét ΔKDB và ΔKEC có
\(\widehat{KDB}=\widehat{KEC}\)
BD=CE
\(\widehat{KBD}=\widehat{KCE}\)
Do đó: ΔKDB=ΔKEC