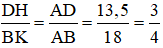Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
⇒ AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Ta-lét ta có:
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4
Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
⇒ AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Ta-lét ta có:
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4


Gọi DE và BF lần lượt là khoảng cách từ B và D đến cạnh AC.
Ta có DE // BF (cùng vuông góc với AC)
Áp dụng hệ quả của định lí ta – lét đối với ΔABF ta có:
Có AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
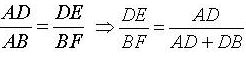

Vậy tỉ số khoảng cách từ điểm D và B đến AC bằng 0,75.
Gọi DH và BK lần lượt là khoảng cách từ B và D đến cạnh AC.
Ta có DH // BK (cùng vuông góc với AC)
=> DHBKDHBK = ADABADAB
Mà AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
Vậy DHBKDHBK = 13,51813,518 = 3434
Vậy tỉ số khoảng cách từ điểm D và B đến AC bằng 34

Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
⇒ AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Ta-lét ta có:
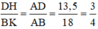
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4

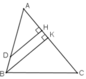
A D H B K C
Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK ( cùng vuông góc với AC ) nên áp dụng hệ quả định lí Ta-lét ta có :
\(\frac{DH}{BK}=\frac{AD}{AB}=\frac{13,5}{18}=\frac{3}{4}\)
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là \(\frac{3}{4}\)

kẻ DH và BG vuông góc AC
=>DH//BG
Xét ΔABG có DH//BG
nên AD/DB=AH/HG=3
=>AH=3HG
=>DH/BG=3/4
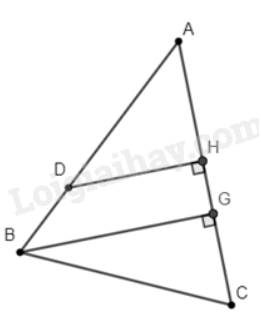
Gọi \(H;G\) lần lượt là hình chiếu vuông góc của \(D;B\)lên \(AC\).
Khi đó, khoảng cách từ \(D\) đến \(AC\) là \(DH\);khoảng cách từ \(B\) đến \(AC\) là \(BG\).
Ta có: \(AB = AD + BD = 13,5 + 4,5 = 18cm\)
Vì \(\left\{ \begin{array}{l}DH \bot AC\\BG \bot AC\end{array} \right. \Rightarrow DH//BG\)
Xét tam giác \(ABG\) có \(DH//BG\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{AB}} = \frac{{DH}}{{BG}} \Leftrightarrow \frac{{13,5}}{{18}} = \frac{{DH}}{{BG}} = \frac{3}{4}\)
Vậy tỉ số khoảng cách từ điểm \(D\) và \(B\) đến đoạn thẳng \(AC\) là \(\frac{3}{4}\).

Gọi DH và BK lần lượt là khoảng cách từ B và D đến cạnh AC.
Ta có DH // BK (cùng vuông góc với AC)
=> \(\frac{DH}{BK}\) = \(\frac{AD}{BC}\)
Mà AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
Vậy \(\frac{DH}{BK}\) = \(\frac{13,5}{18}=\frac{3}{4}\)
Vậy tỉ số khoảng cách từ điểm D và B đến AC bằng

Độ dài cạnh AB là: 3,5 + 14 = 17,5 (cm)
Tỉ số từ điểm B đến cạnh AB là:
3,5 : 17,5 = 1/5 (AB)
Tỉ số từ điểm D đến cạnh AB là:
14 : 17,5 = 4/5 (AB)