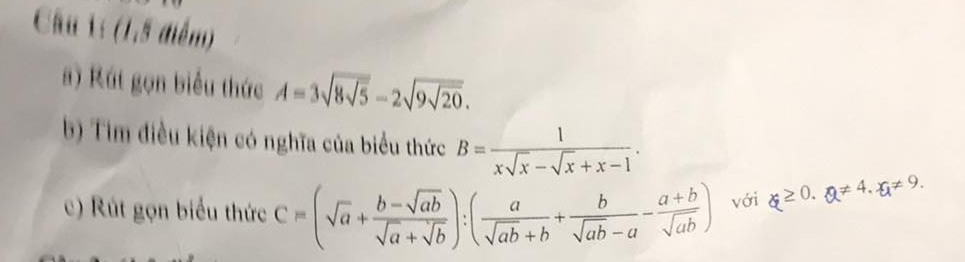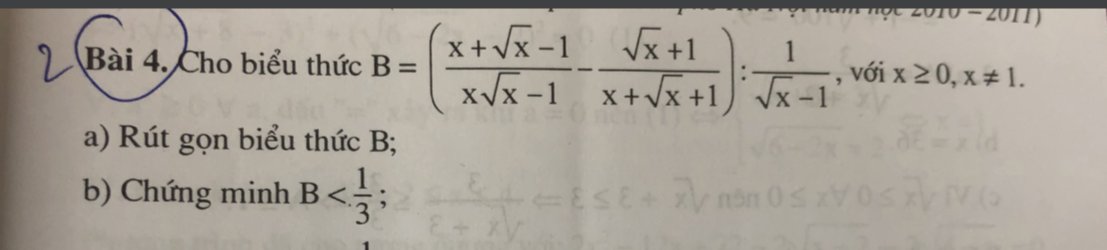Giải hộ e bài 16 câu b vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 6 2023
b: PTHĐGĐ là;
ax^2=2
=>ax^2-2=0
Δ=0^2-4*a*(-2)=8a
Để (P) cắt (d) tại hai điểm pb thì 8a>0
=>a>0
=>x=căn 2/a hoặc x=-căn 2/a
=>vecto OA=(căn 2/a;0); vecto OB=(-căn 2/a;0); vecto AB=(2*căn 2/a;2)
Theo đề, ta có: vecto OA*vecto OB=0 hoặc vecto OA*vecto AB=0 hoặc vecto OB*vecto AB=0
=>-2*căn 2/a+2=0 hoặc 2*căn 2/a+2=0
=>căn 2/a=1
=>a=2
PT
2
HP
19 tháng 10 2021
a. Mg + 2HCl ---> MgCl2 + H2↑
b. Fe2O3 + 6HCl ---> 2FeCl3 + 3H2O
c. 2Al + 6HCl ---> 2AlCl3 + 3H2↑
d. 2C2H6 + 7O2 ---to---> 4CO2↑ + 6H2O
e. BaCl2 + 2AgNO3 ---> Ba(NO3)2 + 2AgCl↓
f. Al2(SO4)3 + 3Ba(OH)2 ---> 2Al(OH)3 + 3BaSO4↓
Trong đó:
to: nhiệt độ
↑: bay hơi
↓: kết tủa
(Câu f sai nên mik sửa từ Al2(SO4)3 thành Al(OH)3)
M
giải hộ mình mấy bài này vs ạ !
2
6 tháng 5 2021
Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
6 tháng 5 2021
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm
NB
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 7 2023
Em đã nhờ thầy cô của olm thì thầy cô của olmcũng sẵn lòng giúp em, cảm ơn em đã yêu thương và tin tưởng olm.vn
Bài 14 của em đây:
y + y \(\times\) \(\dfrac{1}{3}\) : \(\dfrac{2}{9}\) + y : \(\dfrac{2}{7}\) = 252
y + y \(\times\) \(\dfrac{1}{3}\) \(\times\) \(\dfrac{9}{2}\) + y \(\times\) \(\dfrac{7}{2}\) = 252
y + y \(\times\) \(\dfrac{3}{2}\) + y \(\times\) \(\dfrac{7}{2}\) = 252
y \(\times\)( 1 + \(\dfrac{3}{2}\) + \(\dfrac{7}{2}\)) = 252
y \(\times\) 6 = 252
y = 252 : 6
y = 42
VD
25 tháng 5 2022
`#Hưng`
\(a,3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\\ =\sqrt{9.8\sqrt{5}}-\sqrt{4.9\sqrt{20}}\\ =\sqrt{72\sqrt{5}}-\sqrt{36\sqrt{20}}\\ =\sqrt{\sqrt{5184.5}}-\sqrt{\sqrt{1296.20}}\\ =\sqrt{\sqrt{25920}}-\sqrt{\sqrt{25920}}\\ =0\)
\(b,ĐKXĐ:x\sqrt{x}-\sqrt{x}+x-1\ne0\\ \Rightarrow\sqrt{x}\left(x-1\right)+\left(x-1\right)\ne0\\ \Rightarrow\left(x-1\right)\left(\sqrt{x}+1\right)\ne0\\ \Rightarrow x-1\ne0\left(vì.\sqrt{x}+1>0\right)\\ \Rightarrow x\ne1\)
22 tháng 7 2023
a: \(B=\dfrac{x+\sqrt{x}-1-x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
b: \(B-\dfrac{1}{3}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{3}\)
\(=\dfrac{3\sqrt{x}-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(\sqrt{x}+1\right)^2}{3\left(x+\sqrt{x}+1\right)}< 0\)
=>B<1/3
