vẽ hình lun ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


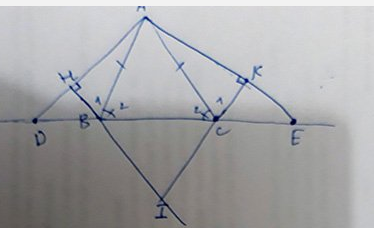
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
Suy ra: BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
Do đó: ΔAHB=ΔAKC

1:
Ta có: ΔABC vuông tại C
mà ΔCAB nội tiếp (O)
nên O là trung điểm của AB
Xét tứ giác OBDC có \(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)
nên OBDC là tứ giác nội tiếp
=>O,B,D,C cùng thuộc một đường tròn
Xét (O) có
DC,DB là các tiếp tuyến
Do đó: DC=DB
=>D nằm trên đường trung trực của CB(1)
Ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1) và (2) suy ra OD là đường trung trực của CB
=>OD\(\perp\)CB
Ta có: AC\(\perp\)CB
CB\(\perp\)OD
Do đó: OD//AC
2: Xét (O) có
ΔBEA nội tiếp
AB là đường kính
Do đó: ΔBAE vuông tại E
=>BE\(\perp\)EA tại E
=>BE\(\perp\)AD tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(DE\cdot DA=DB^2\left(3\right)\)
Xét ΔDOB vuông tại B có BH là đường cao
nên \(DH\cdot DO=DB^2\)(4)
Từ (3) và (4) suy ra \(DE\cdot DA=DH\cdot DO\)

a: Xet ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
góc ABD=góc MBD
=>ΔBAD=ΔBMD
b: AD=DM
DM<DC
=>AD<CD
c: Xét ΔDAK vuông tại A và ΔDMC vuông tại M có
DA=DM
góc ADK=góc MDC
=>ΔDAK=ΔDMC
=>AK=MC: DK=DC
=>ΔDKC cân tại D; BK=BC
=>ΔBKC can tại B
mà BN là phân giác
nên BN vuông góc KC

b: Xét ΔDEM và ΔDFM có
DE=DF
\(\widehat{EDM}=\widehat{FDM}\)
DM chung
Do đó: ΔDEM=ΔDFM
c: Xét ΔDEF có
DM là đường trung tuyến
G là trọng tâm
Do đó: D,G,M thẳng hàng

Bài 4:
a: \(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)
b: Xét ΔEDB có
EA là đường cao
EA là đường trung tuyến
Do đó:ΔEDB cân tại E
Xét ΔCDB có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCDB cân tại C
Xét ΔCDE và ΔCBE có
CD=CB
ED=EB
CE chung
Do đó: ΔCDE=ΔCBE
c: Xét ΔCDB có
CA là đường trung tuyến
CE=2/3CA
Do đó: E là trọng tâm của ΔCDB
Suy ra: DE đi qua trung điểm của BC



a: XétΔAHB vuông tại H và ΔAKC vuông tạiK có
góc A chung
=>ΔAHB đồng dạng với ΔAKC
b: góc BKC=góc BHC=90 độ
=>BKHC nội tiếp
=>góc AKH=góc ACB
mà góc A chung
nên ΔAKH đồng dạng với ΔACB

=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ

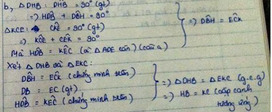
 có vẽ hình lun ạ
có vẽ hình lun ạ


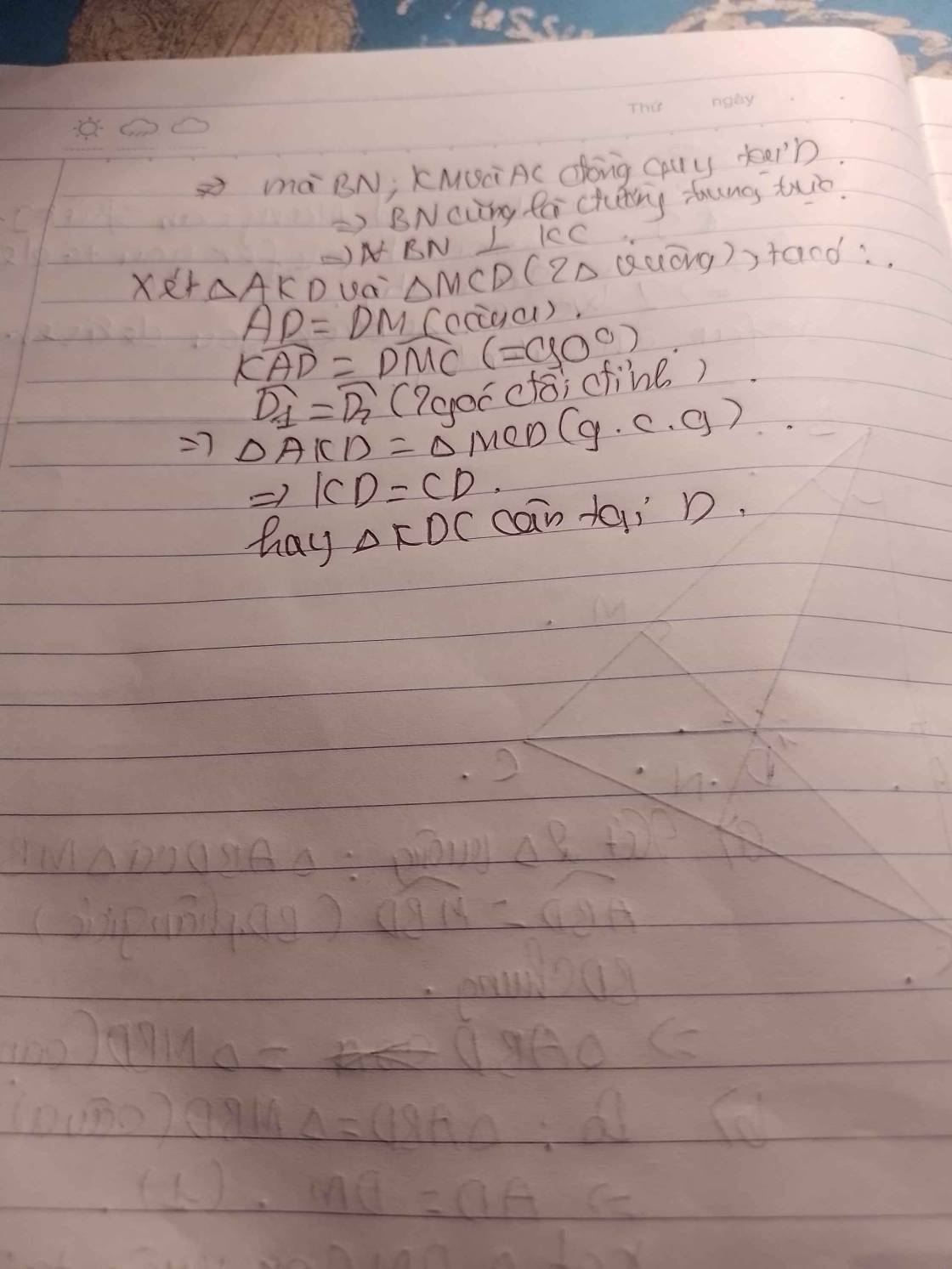







 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
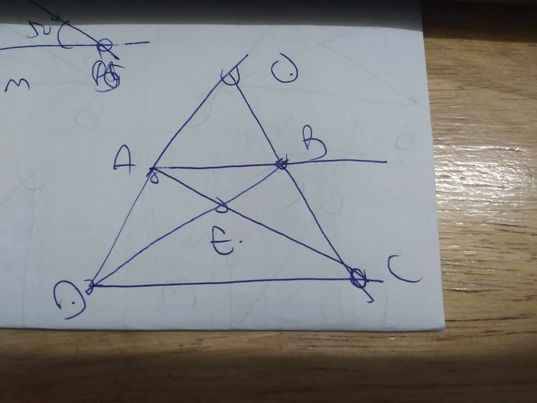
1: Xét tứ giác OBPC có
\(\widehat{OBP}+\widehat{OCP}=90^0+90^0=180^0\)
=>OBPC là tứ giác nội tiếp
=>O,B,P,C cùng thuộc một đường tròn
2: Xét (O) có
PC,PB là các tiếp tuyến
Do đó: PC=PB
=>P nằm trên đường trung trực của CB(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OP là đường trung trực của BC
=>OP\(\perp\)BC
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB
Ta có: AC\(\perp\)CB
OP\(\perp\)CP
Do đó: AC//OP