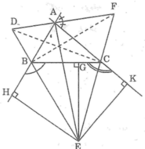
Cho \(\Delta\)ABC, phân giác góc trong và góc ngoài của \(\widehat{B}\)và gặp nhau theo thứ tự ở I và J. Từ J kẻ JH ; JP; JK lần lượt vuông góc với AB;BC;AC
1. Chứng minh : A;I;J thẳng hàng
2. C/M : BỊCJ nội tiếp
3. BI kéo dài cắt đt CJ tại E . c/m: AE \(⊥\)AJ
4. C/M : AI.AJ=AB.AC