1) Cho hình bình hành ABCD. trên cạnh BC lấy điểm G, trên cạnh AD lây điểm H sao cho CG=AH.
Cmr: Các đường thẳng GH, AC, BD đồng quy
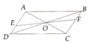
2) Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. E và F theo thứ tự là trung điểm của OB và OD
a) Cmr: AE// CF
b) Gọi K là giao điểm của AE và DC. Cmr DK=1/2 KC
3) Cho tam giác ABC, trực tâm H. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C, cắt nhau tại D
Cmr: a) BDCH là hình bình hành
b) BAD+ BDC= 180o
c) Ba điểm H,M,D thẳng hàng ( M là trung điểm của BC)
d) OM= 1/2 AH ( O là trung điểm của AD)
MỌI NGƯỜI GIẢI NHANH HỘ MK VỚI AK, MAI MK NỘP BÀI RỒI. CẢM ƠN NHÌU AK

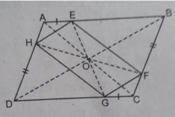
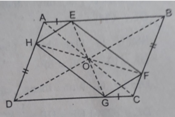
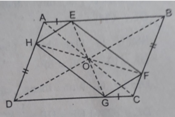
1. \(ABCD\)là hbh nên AC và BD cắt nhau tại trung điểm mỗi đường
AH//CG, AH=CG nên AHCG là hbh (dhnb) => AC và HG cắt nhau tại trung điểm mỗi đường
Vậy AC, HG, BD đồng quy tại TRUNG ĐIỂM mỗi đường
2.a) Có O là trung điểm của BD và AC nên OA=OC và OE=OF
Do đó AC cắt EF tại trugn điểm mỗi đường nên AECF là hbh (dhnb)
nên AE//CF (đpcm).
b) Còn câu b) là thế nào???