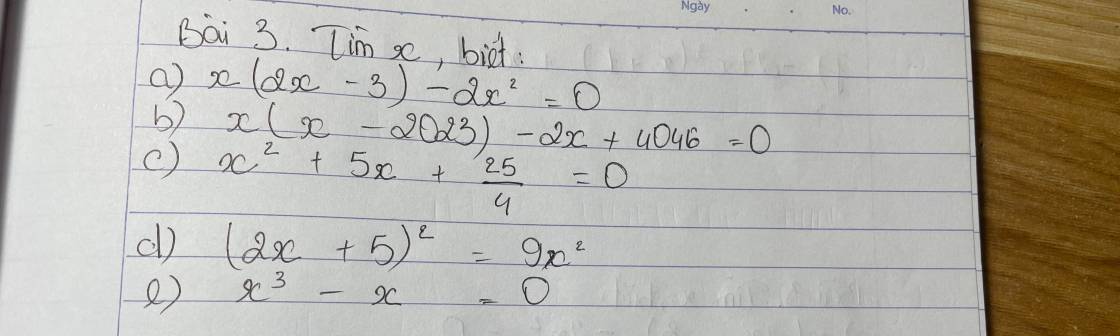 giải giúp e với ạa (bỏ câu a)
giải giúp e với ạa (bỏ câu a)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)
\(\Leftrightarrow\sqrt{x-2}=10\)
\(\Leftrightarrow x-2=100\)
\(\Leftrightarrow x=102\)

a: Khi m=-2 thì (d): y=-5x-2
ii: Tọa độ giao điểm của (P) và (d) là:
\(\left\{{}\begin{matrix}2x^2+5x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{-\dfrac{1}{2};-2\right\}\\y\in\left\{\dfrac{1}{2};8\right\}\end{matrix}\right.\)
Vậy: M(-1/2;1/2); N(-2;8)
\(OM=\sqrt{\left(-\dfrac{1}{2}-0\right)^2+\left(\dfrac{1}{2}-0\right)^2}=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}=\dfrac{\sqrt{2}}{2}\)
\(ON=\sqrt{\left(-2-0\right)^2+\left(8-0\right)^2}=2\sqrt{17}\)
\(MN=\sqrt{\left(-2+\dfrac{1}{2}\right)^2+\left(8-\dfrac{1}{2}\right)^2}=\sqrt{\dfrac{9}{4}+\dfrac{225}{4}}=\dfrac{3\sqrt{26}}{2}\)
\(P=OM+ON+NM\simeq4,93\left(cm\right)\)
\(S=\sqrt{4,93\cdot\left(4,93-\dfrac{\sqrt{2}}{2}\right)\cdot\left(4.93-2\sqrt{17}\right)\left(4.93-\dfrac{3\sqrt{26}}{2}\right)}=13,7\left(cm^2\right)\)

Với m=-2
Phương trình tọa độ giao điểm của (d) và (P) là:
\(2x^2=\left(-2-3\right)x+\left(-2\right)\Leftrightarrow2x^2+5x+2=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{1}{2}\\y=8\end{matrix}\right.\)
Gọi \(M\left(-\dfrac{1}{2};\dfrac{1}{2}\right),N\left(-2;8\right)\) và kẻ \(NH\perp MO\) ta có hình vẽ như sau:
Gọi phương trình đường thẳng MO là: ax+b=y
\(\left\{{}\begin{matrix}a.0+b=0\\-2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=-4\end{matrix}\right.\)
Phương trình đường thẳng MO là: -4x=y
Gọi phương trình đường thẳng NH là: ax+b=y
Để NH vuông góc với MO thì: a.a'=-1 \(\Leftrightarrow a.\left(-4\right)=-1\Leftrightarrow a=\dfrac{1}{4}\)
Ta có: \(y=\dfrac{1}{4}x+b\Leftrightarrow\dfrac{1}{2}=\dfrac{1}{4}.\dfrac{-1}{2}+b\Rightarrow b=\dfrac{5}{8}\)
Phương trình đường thẳng NH là: \(y=\dfrac{1}{4}x+\dfrac{5}{8}\)
Phương trình tọa độ giao điểm của NH và MO là: \(-4x=\dfrac{1}{4}x+\dfrac{5}{8}\Leftrightarrow x=\dfrac{-5}{34}\Rightarrow y=\dfrac{10}{17}\)
Độ dài đoạn NH là: NH= \(\sqrt{\left(-\dfrac{5}{34}--\dfrac{1}{2}\right)^2+\left(\dfrac{10}{17}-\dfrac{1}{2}\right)^2}=\dfrac{3\sqrt{17}}{34}\)
Độ dài đoạn MO là: MO=\(\sqrt{\left(-2-0\right)^2+\left(8-0\right)^2}=2\sqrt{17}\)
Diện tích tam giác OMN là: \(S=\dfrac{1}{2}NH.OM=\dfrac{1}{2}.\dfrac{3\sqrt{17}}{34}.2\sqrt{17}\)=1,5(đvdt)

1. PTBD: Biểu cảm
2. NDC: Nói về những điều tốt đẹp trong truyện cổ và tình cảm của tác giả dành cho truyện cổ
3. ''Thương người rồi mới thương ta''
''Ở hiền thì lại gặp hiền
4. Có đồng ý vì truyện cổ là những truyện đã có từ xưa, những gì diễn ra trong lịch sử. Khi nghe truyện cổ, ta mới biết thêm về ông cha ta và những điều hay ý đẹp đã có từ trước đây.


1 are making
2 is running - wants
3 is
4 went
5 writes
6 was playing - arrived
7 is doing
8 will just come - see
9 will come - are you
10 did you go
11 haven't left - went
12 will come
13 met - have already decided
14 have never seen
15 bloom
16 haven't lived


a: 5 không là số nguyên tố
b: 4+x>=3
c: (căn 3+căn 12)^2 là số vô tỉ
d: Phương trình x^2+2023x=1 có nghiệm
e: 3^2+4^2<>5^2
f: căn 3*căn 27<>9
g: x=1 không là nghiệm của phương trình \(\dfrac{x^2-1}{x-1}=0\)
h: Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại









 giúp e với ạa
giúp e với ạa
3d.
$(2x+5)^2=9x^2$
$\Leftrightarrow (2x+5)^2-(3x)^2=0$
$\Leftrightarrow (2x+5-3x)(2x+5+3x)=0$
$\Leftrightarrow (-x+5)(5x+5)=0$
$\Leftrightarrow -x+5=0$ hoặc $5x+5=0$
$\Leftrightarrow x=5$ hoặc $x=-1$
3b.
$x(x-2023)-2x+4046=0$
$\Leftrightarrow x(x-2023)-2(x-2023)=0$
$\Leftrightarrow (x-2023)(x-2)=0$
$\Leftrightarrow x-2023=0$ hoặc $x-2=0$
$\Leftrightarrow x=2023$ hoặc $x=2$
3c.
$x^2+5x+\frac{25}{4}=0$
$\Leftrightarrow x^2+2.x.\frac{5}{2}+(\frac{5}{2})^2=0$
$\Leftrightarrow (x+\frac{5}{2})^2=0$
$\Leftrightarrow x+\frac{5}{2}=0$
$\Leftrightarrow x=\frac{-5}{2}$