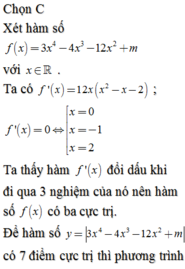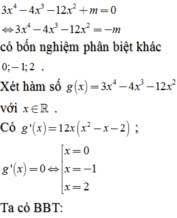Câu 48/Đề 7: Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] đêể bất phương trình log3(x2+x+1)+2x3 ≤ 3x2 + log3x +m-1 có ít nhất 2 nghiệm phân biệt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để tìm số giá trị nguyên của m trong khoảng [-10;10] sao cho giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3] nhỏ hơn 10, chúng ta cần thực hiện các bước sau:
1. Tìm giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3].
2. Kiểm tra xem giá trị lớn nhất của hàm số có nhỏ hơn 10 hay không.
3. Đếm số giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện trên.
Bước 1: Tìm giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3].
Để tìm giá trị lớn nhất, chúng ta có thể lấy đạo hàm của hàm số và giải phương trình đạo hàm bằng 0.
y' = -4x^3 + 4
Để tìm giá trị của x khi đạo hàm bằng 0, giải phương trình:
-4x^3 + 4 = 0
X^3 - 1 = 0
( x - 1)( x^2 + x + 1) = 0
Phương trình có 2 nghiệm: x = 1 và x^2 + x + 1 =0 (phương trình bậc 2).
Bước 2: Kiểm tra giá trị lớn nhất của hàm số có nhỏ hơn 10 hay không.
Để kiểm tra giá trị lớn nhất của hàm số, chúng ta có thể thay x = 1 vào hàm số:
y = - 1^4(1) - m = 3 - m
Điều kiện y < 10:
3 - m < 10
- m < 7
m > -7
Bước 3: Đếm số giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện trên.
Trong khoảng [-10;10], có 17 giá trị nguyên. Tuy nhiên, chúng ta chỉ quan tâm đến các giá trị m > -7.
Vậy, có 17 - 7 = 10 giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện y < 10.

Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A

Chọn D.
Phương pháp: Biện luận nghiệm của phương trình theo m.
Cách giải: Ta có:
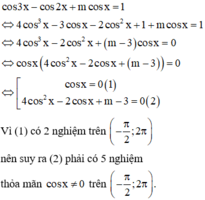

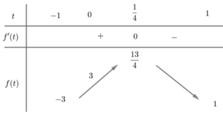


Đáp án D.
Đặt
f x = 3 x 4 − 4 x 3 − 12 x 2 → f ' x = 12 x 3 − 12 x 2 − 24 x , ∀ x ∈ ℝ .
Khi đó y = f x + m ⇒ y ' = f ' x . f x + m f x + m .
Phương trình y ' = 0 ⇔ f ' x = 0 f ' x = − m ( * )
Để hàm số đã cho có 7 điểm cực trị
⇔ y ' = 0 có 7 nghiệm phân biệt.
Mà f ' x = 0 có 3 nghiệm phân biệt
⇒ f x = − m có 4 nghiệm phân biệt.
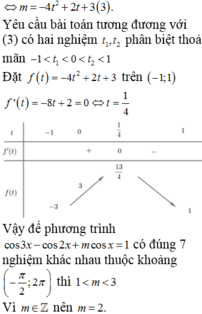
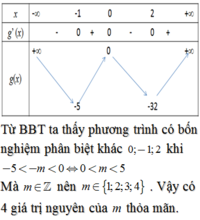
Dựa vào BBT hàm số f x , đẻ (*) có 4 nghiệm phân biệt
⇔ − 5 < − m < 0 ⇔ m ∈ 0 ; 5 .
Kết hợp với m ∈ ℤ suy ra có tất cả 4 giá trị nguyên cần tìm.

Đáp án D
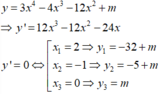
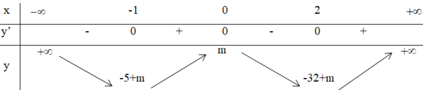
Dựa vào BBT để hàm số y = 3 x 4 − 4 x 3 − 12 x 2 + m có 7 điểm cực trị thì: