Cho tam giác ABC nhọn, đường tròn tâm O đường kính BC cắt AB tại D và cắt AC tại E. Gọi D' ; E' lần lượt là điểm đối xứng của D;E qua O.C/m :
a/ Hình lục giác BDECD'E' nội tiếp đường tròn tâm O
b/H là trực tâm tam giác ABC.C/m HD.BD'= AD.BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 1 2019
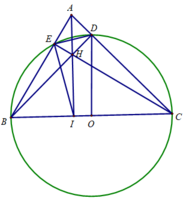
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = B C 2 = 16 2 = 256
22 tháng 1 2022
a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
b: Ta có: H là trực tâm của ΔABC
nên AH⊥BC tại F
Xét ΔAEH vuông tại E và ΔAFB vuông tại F có
\(\widehat{EAH}\) chung
Do đó: ΔAEH\(\sim\)ΔAFB
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AH}{AB}\)
hay \(AE\cdot AB=AF\cdot AH\left(1\right)\)
Xét ΔADH vuông tại D và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔADH\(\sim\)ΔAFC
Suy ra: \(\dfrac{AD}{AF}=\dfrac{AH}{AC}\)
hay \(AD\cdot AC=AH\cdot AF\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AH\cdot AF=AD\cdot AC\)
18 tháng 3 2021
Sửa đề: BF và CE cắt nhau tại H
a) Xét (O) có
ΔBEC nội tiếp đường tròn(B,E,C\(\in\)(O))
BC là đường kính(gt)
Do đó: ΔBEC vuông tại E(Định lí)
\(\Leftrightarrow CE\perp BE\)
\(\Leftrightarrow CE\perp AB\)
\(\Leftrightarrow\widehat{AEC}=90^0\)
hay \(\widehat{AEH}=90^0\)
Xét (O) có
ΔBFC nội tiếp đường tròn(B,F,C\(\in\)(O))
BC là đường kính(gt)
Do đó: ΔBFC vuông tại F(Định lí)
\(\Leftrightarrow BF\perp CF\)
\(\Leftrightarrow BF\perp AC\)
\(\Leftrightarrow\widehat{AFB}=90^0\)
hay \(\widehat{AFH}=90^0\)
Xét tứ giác AEHF có
\(\widehat{AEH}\) và \(\widehat{AFH}\) là hai góc đối
\(\widehat{AEH}+\widehat{AFH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét ΔABC có
BF là đường cao ứng với cạnh AC(cmt)
CE là đường cao ứng với cạnh AB(cmt)
BF cắt CE tại H(gt)
Do đó: H là trực tâm của ΔABC(Định lí ba đường cao của tam giác)
\(\Leftrightarrow AH\perp BC\)
hay \(AD\perp BC\)(đpcm)