K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
17 tháng 2 2018
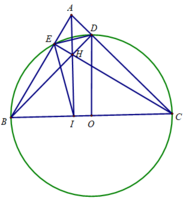
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)

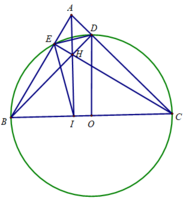
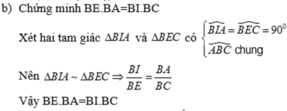
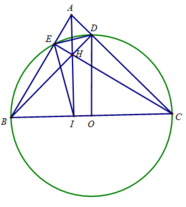

d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = B C 2 = 16 2 = 256