Phương trình 3×2^x -4^x-2=0 có 2 nghiệm x1,x2.Tính tổng x1+x2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=-3\end{matrix}\right.\)
\(x_1^3x_2+x_2^3x_1=x_1x_2\left(x^2_1+x_2^2\right)=x_1x_2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\)
\(=-3.\left(1^2-2.\left(-3\right)\right)=-21\)
`Delta=1+12=13>0`
`=>` pt có 2 nghiệm pb
Áp dụng vi-ét:`x_1+x_2=1,x1.x_2=-3`
`=>x_1^3x_2+x_1x_2^3`
`==x_1.x_2(x_1^2+x_2)^2`
=-3[(x_1+x_2)^2-2.x_1.x_2]`
`=-3(1+6(`
`=-3.7`
`=-21`

Phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )

c) Ta có: \(\text{Δ}=\left[-2\left(m+1\right)\right]^2-4\cdot1\cdot\left(2m+1\right)\)
\(=\left(-2m-2\right)^2-4\left(2m+1\right)\)
\(=4m^2+8m+4-8m-4\)
\(=4m^2\ge0\forall m\)
Do đó, phương trình luôn có nghiệm
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+1\right)}{1}=2m+2\\x_1\cdot x_2=2m+1\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1-2x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2=2m-1\\x_1=2m+2+x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{2m-1}{3}\\x_1=2m+3+\dfrac{2m-1}{3}=\dfrac{8m+8}{3}\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=2m+1\)
\(\Leftrightarrow\dfrac{2m-1}{3}\cdot\dfrac{8m+8}{3}=2m+1\)
\(\Leftrightarrow\left(2m-1\right)\left(8m+8\right)=9\left(2m+1\right)\)
\(\Leftrightarrow16m^2+16m-8m-8-18m-9=0\)
\(\Leftrightarrow16m^2-10m-17=0\)
\(\text{Δ}=\left(-10\right)^2-4\cdot16\cdot\left(-17\right)=1188\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{10-6\sqrt{33}}{32}\\m_2=\dfrac{10+6\sqrt{33}}{32}\end{matrix}\right.\)

a.
\(\Delta=m^2-4\left(2m-4\right)=m^2-8m+16=\left(m-4\right)^2\ge0;\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=2m-4\end{matrix}\right.\)
c.
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow m^2-2\left(2m-4\right)=4\)
\(\Leftrightarrow m^2-4m+4=0\Rightarrow m=2\)
a.\(\Delta=m^2-4\left(2m-4\right)=m^2-8m+16=\left(m-4\right)^2\ge0\)
=> pt luôn có nghiệm với mọi m
b.Theo hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1.x_2=2m-4\end{matrix}\right.\)
c.\(x_1^2+x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=4\)
\(\Leftrightarrow\left(-m\right)^2-2\left(2m-4\right)=4\)
\(\Leftrightarrow m^2-4m+8-4=0\)
\(\Leftrightarrow m^2-4m+4=0\)
\(\Leftrightarrow\left(m-2\right)^2=0\)
\(\Leftrightarrow m=2\)

\(\Delta'=\left(m-2\right)^2+5>0;\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\x_1x_2=-5\end{matrix}\right.\)
\(\left|\left|x_1\right|-\left|x_2\right|\right|=4\)
\(\Leftrightarrow\left(\left|x_1\right|-\left|x_2\right|\right)^2=16\)
\(\Leftrightarrow x_1^2+x_2^2-2\left|x_1x_2\right|=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|=16\)
\(\Leftrightarrow4\left(m-2\right)^2-2.\left(-5\right)-2.\left|-5\right|=16\)
\(\Leftrightarrow\left(m-2\right)^2=4\)
\(\Rightarrow\left[{}\begin{matrix}m-2=2\\m-2=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=4\\m=0\end{matrix}\right.\)

phương trình: x^2-(m+1)x+2m-2=0 (1)
phương trình(1) là ptbh ẩn x có:đen ta = (-(m+1))^2 -4.1.(2m-2) =m^2+2m+1-8m+8 =m^2-6m+9 = (m-3)^2 với mọi m thuộc r
phương trình (1) có 2 nghiệm pb khi và chỉ khi đen ta lớn hơn 0 suy ra (m-3)^2 lớn hơn 0
khi và chỉ khi m-3 lớn hơn 0. ki và chỉ khi m lớn hơn 3.
theo hệ thức vi ét ta có x1+x2=m+1 (2) ;x1.x2=2m-2 (3)
có 3(x1+x2)-X1.X2=10 (4)
từ (2) (3) (4) suy ra 3(m+1)-(2m-2)=10
khi và chỉ khi 3m+3-2m+2=10
khi và chỉ khi m+5=10
khi và chỉ khi m=5
vậy khi m=5 thì pt(1) có 2n pb x1,x2 thỏa mãn 3(x1+x2)-x1.x2=10
Cách 1:
Từ pt ta có:
\(\Delta=\left(m-3\right)^2>0\)
=>x1=(m-1-m+3)/2=1
->x2=(m-1+m-2)/2=(2m-3)/2
Bạn thay x1,x2 vào rồi tính nha tới đây thì đơn giản rồi.
Cách 2:
từ pt ta có:
\(\hept{\begin{cases}\Delta=\left(m-3\right)^2>0\\x_1+x_2=m-1\\x_1x_2=2-2m\end{cases}}\)
Bạn cũng thay vào rồi tính nha.
Đúng thì nhớ k cho mình nha.

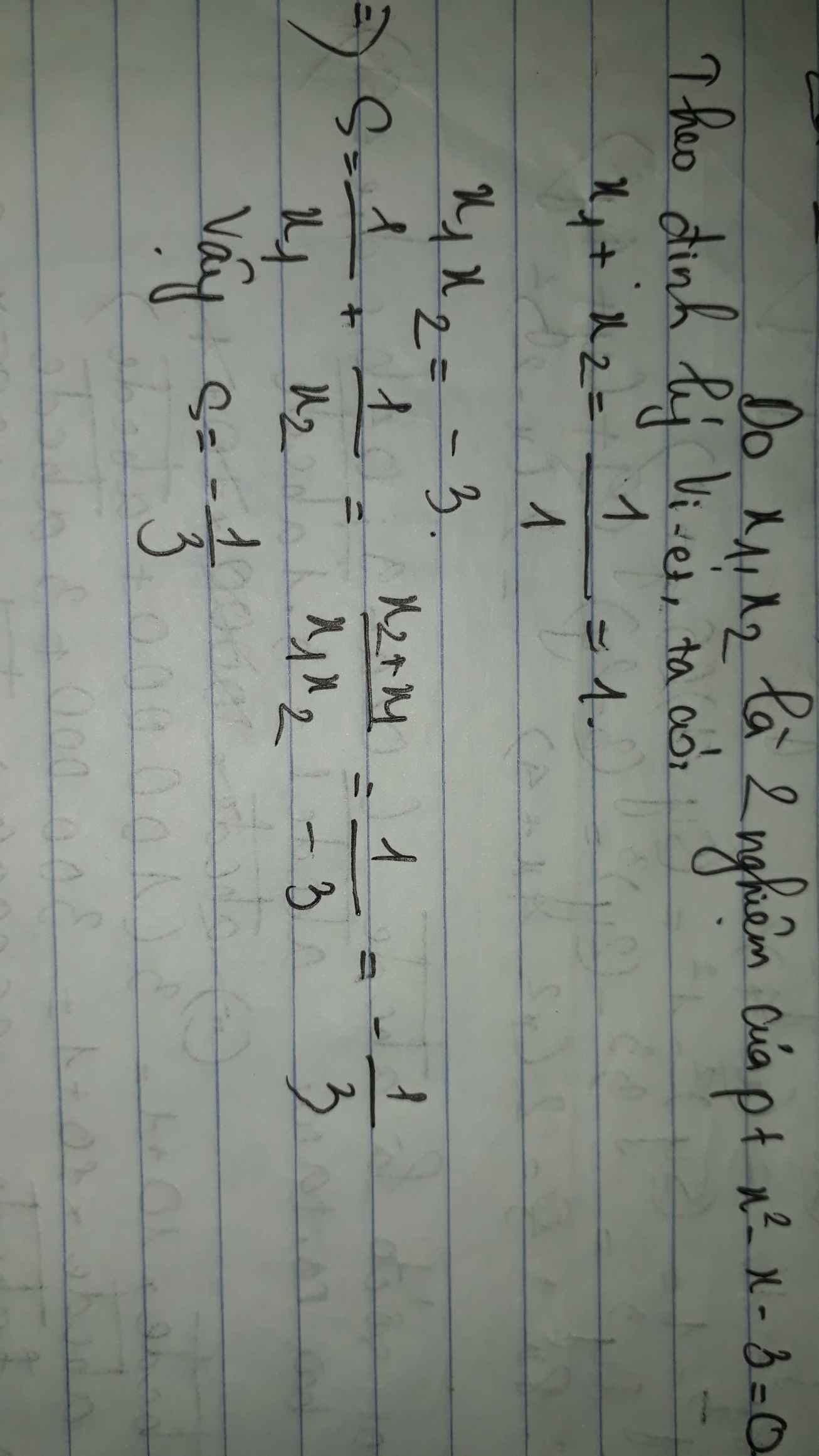
Đặt \(t=2^x\)
Phương trình sẽ trở thành:
\(-t^2+3t-2=0\)
=>\(\left(t^2-3t+2\right)=0\)
=>\(\left(t-1\right)\left(t-2\right)=0\)
=>\(\left[{}\begin{matrix}t=1\\t=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2^x=1\\2^x=2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(x_1+x_2=0+1=1\)