LN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
20 tháng 5 2017
Đáp án D.
ĐK: x > 2.
TH1: Ta thấy x = 3 không phải là nghiệm của PT.
TH2: Với x ≠ 3 logarit cơ số x – 2 cả 2 vế ta được
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1
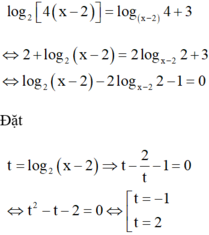
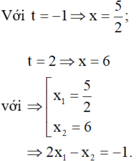
\(\Leftrightarrow\left(\dfrac{3}{4}\right)^x.\left(\dfrac{4}{3}\right)^{\dfrac{4}{x}}=\dfrac{9}{16}\)
\(\Rightarrow\left(\dfrac{3}{4}\right)^x.\left(\dfrac{3}{4}\right)^{-\dfrac{4}{x}}=\left(\dfrac{3}{4}\right)^2\)
\(\Rightarrow\left(\dfrac{3}{4}\right)^{x-\dfrac{4}{x}}=\left(\dfrac{3}{4}\right)^2\)
\(\Rightarrow x-\dfrac{4}{x}=2\)
\(\Rightarrow x^2-2x-4=0\)
Viet: \(x_1+x_2=2\)
CM
4 tháng 12 2018
Đáp án D
Phương pháp:
Đặt 2x = t, t > 0. Chuyển về bài toán tìm m để phương trình bậc 2 ẩn t có 2 nghiệm t1, t2 thỏa mãn t1.t2 = 8
Cách giải:
Để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 + x2 = 3 thì phương trình (2) có 2 nghiệm t1,t2 thỏa mãn t1.t2 = 2x1.2x2 = 2x1 + x2 = 23 = 8
Khi đó:
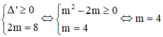
Đặt \(t=2^x\)
Phương trình sẽ trở thành:
\(-t^2+3t-2=0\)
=>\(\left(t^2-3t+2\right)=0\)
=>\(\left(t-1\right)\left(t-2\right)=0\)
=>\(\left[{}\begin{matrix}t=1\\t=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2^x=1\\2^x=2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(x_1+x_2=0+1=1\)