Chứng minh rằng: 32 + 33+ 34 +……+ 3101 chia hết cho 120
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 32 + 33 + 34 +...+ 3101
A = 32.(1 + 3 + 32 + 33 +...+ 399)
A =32[(1+ 3+32+33) + (34+ 35+36+37)+...+ (396 + 397+ 398 + 399)
A = 32.[ 40 + 34.(1+ 3 + 32 + 33)+...+ 396.(1 + 3 + 32 + 33)
A = 32.[ 40 + 34. 40 + ...+ 396.40]
A = 32.40.[ 1 + 34+...+396]
A = 3.120.[1 + 34 +...+ 396]
120 ⋮ 120 ⇒ A = 3.120.[ 1 + 34 +...+396] ⋮ 120 (đpcm)

`#3107.101107`
\(A=1+3+3^2+3^3+...+3^{101}\)
$A = (1 + 3 + 3^2) + (3^3 + 3^4 + 3^5) + ... + (3^{99} + 3^{100} + 3^{101}$
$A = (1 + 3 + 3^2) + 3^3 (1 + 3 + 3^2) + ... + 3^{99}(1 + 3 + 3^2)$
$A = (1 + 3 + 3^2)(1 + 3^3 + ... + 3^{99})$
$A = 13(1 + 3^3 + ... + 3^{99})$
Vì `13(1 + 3^3 + ... + 3^{99}) \vdots 13`
`\Rightarrow A \vdots 13`
Vậy, `A \vdots 13.`
\(A=1+3+3^2+3^3+3^4+3^5+...+3^{101}\\=(1+3+3^2)+(3^3+3^4+3^5)+(3^6+3^7+3^8)+...+(3^{99}+3^{100}+3^{101})\\=13+3^3\cdot(1+3+3^2)+3^6\cdot(1+3+3^2)+...+3^{99}\cdot(1+3+3^2)\\=13+3^3\cdot13+3^6\cdot13+...+3^{99}\cdot13\\=13\cdot(1+3^3+3^6+...+3^{99})\)
Vì \(13\cdot(1+3^3+3^6...+3^{99}\vdots13\)
nên \(A\vdots13\)
\(\text{#}Toru\)



\(A=3+3^2+3^3+3^4+.......+3^{100}\)
\(\Rightarrow A=\left(3+3^2+3^3+3^4\right)+.......+\left(3^{97}+3^{98}+3^{99}+3^{100}\right)\)
\(\Rightarrow A=3.\left(1+3+3^2+3^3\right)+........+3^{97}.\left(1+3+3^2+3^3\right)\)
\(\Rightarrow A=3.40+.........+3^{97}.40\)
\(\Rightarrow A=40.\left(3+.......+3^{97}\right)\)
\(\Rightarrow A⋮40\)( 1 )
Vì \(A\)là tổng của các bậc lũy thừa của 3 nên \(A⋮3\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra : \(A⋮40.3\)
\(\Rightarrow A⋮120\)
Vậy \(A⋮120\)( ĐPCM )

\(A=1+3+3^2+...+3^{101}\)
\(=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+...+\left(3^{99}+3^{100}+3^{101}\right)\)
\(=\left(1+3+3^2\right)+3^3\left(1+3+3^2\right)+...+3^{99}\left(1+3+3^2\right)\)
\(=13\left(1+3^3+...+3^{99}\right)⋮13\)

a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5

A = 8⁸ + 2²⁰
= (2³)⁸ + 2²⁰
= 2²⁴ + 2²⁰
= 2²⁰.(2⁴ + 1)
= 2²⁰.17 ⋮ 17
Vậy A ⋮ 17
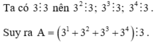
Đặt A = 32 + 33 + 34 + .....+ 3101 ( có 100 số ; có 100 chia hết cho 4 )
A = ( 32 + 33 + 34 + 35 ) + ( 36 + 37 + 38 + 39 ) + ....+ ( 398 + 399 + 3100 + 3101 )
A = 3 . ( 3 + 32 + 33 + 34 ) + 35. ( 3 + 32 + 33 + 34 ) + ..... + 397. ( 3 + 32 + 33 + 34 )
A = 3 . 120 + 35. 120 + .... + 397. 120
A = 120 . ( 3 + 35 + ... + 397 ) chia hết cho 120
\(\Rightarrow\) 32 + 33+ 34 +……+ 3101 chia hết cho 120
tự tím nha