cho đường thẳng (d):y=2x+1
a) vẽ đường thẳng (d)
b)tính diện tích tam giác được tạo thành giữa đường thẳng (d) và hai trục tọa độ
c) tính khoảng cách từ gốc O đến đường thẳng (d)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu a em tự học thành tài nhé
b.
+) Giao điểm giữa (d) và Ox là: A( a; 0)
=> 0 = \(\frac{3}{4}\)a - 3 => a = 4
=> A (4; 0) => OA = |4 | = 4
+ Giao điểm giữa (d) và Oy là: B( 0; b)
=> b = \(\frac{3}{4}\).0 - 3 => b = -3
=> B (0; -3) => OB = | - 3| = 3
Xét tam giác OAB vuông tại O => S (OAB) = \(\frac{1}{2}.OA.OB=\frac{1}{2}.3.4=6\left(đ.v.d.t\right)\)
c. Kẻ OH vuông AB => OH là khoảng cách từ O đến (d)
=> \(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{3^2}+\frac{1}{4^2}=\frac{25}{144}\)
=> OH = 2,4
Vậy khoảng cách từ O đến (d) là 2,4

Bài 1:
b: Thay y=0 vào (d2), ta được:
4x+1=0
hay \(x=-\dfrac{1}{4}\)
Vậy: \(A\left(-\dfrac{1}{4};0\right)\)
Thay x=0 vào (d2), ta được:
\(y=4\cdot0+1=1\)
Vậy: B(0;1)

2: Gọi A,B lần lượt là giao của (d) với trục Ox,Oy
Tọa độ A là:
y=0 và -5x+3=0
=>x=3/5 và y=0
Tọa độ B là:
x=0 và y=-5*0+3=3
=>A(3/5;0); B(0;3)
=>OA=0,6; OB=3
tan a=-5
=>a=101 độ

Gợi ý :
a) y = 2 => x = 2 hoặc -2 ( do có thể < 0 hay > 0 )
b) S(OAB) = 1 => |x| = 1 => x = 1 hoặc -1
c) Gọi khoảng cách từ O tới (d) là OH
OH bé hơn hoặc bằng khoảng cách 2 của O tới điểm cố định trên Oy
=> max = 2 khi d song^2 Ox => x = 0 => đúng mọi m
d) Thay vào biểu thức hệ thức lượng => khoảng cách từ O tới điểm mà d cắt trên Ox là 0 => d trùng Oy
e) thay x vào có kết quả
f) cắt tại điểm > 2 => biểu thức biểu diễn x > 2 ( -2/(m+3) )

* Giao điểm với trục Ox:
Ta có: -2x + 3 = 0
⇔ 2x = 3
⇔ x = 3/2
⇒ A(3/2; 0) là giao điểm với trục Ox
* Giao điểm với trục Oy:
x = 0 ⇔ y = 3
⇒ B(0; 3) là giao điểm với trục Oy
* Khoảng cách từ O(0; 0) tới (d):
Xét đồ thị:
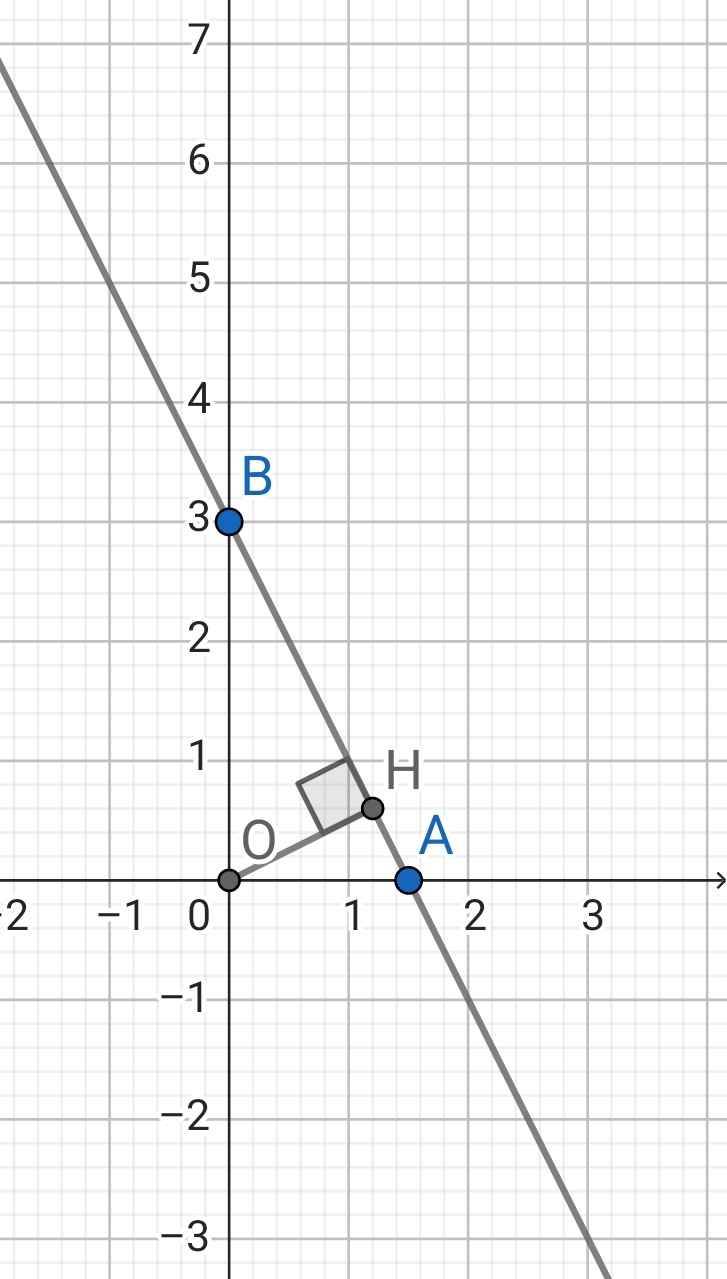 Ta có:
Ta có:
AB² = OA² + OB² (Pytago)
= (3/2)² + 3²
= 45/4
⇒ AB = 3√5/2
Khoảng cách từ O đến (d) là đoạn thẳng OH
Ta có:
OH.AB = OA.OB
⇒ OH = OA.OB : AB
= 3/2 . 3 : (3√5/2)
= 3/√5
a) Ta có: \(y=2x+1\)
\(+)a=2>0;b=1\)
Đồ thị hàm số cắt: \(Ox\left(-\dfrac{1}{2};0\right);Oy\left(0;1\right)\)
b) Gọi giao điểm của hàm số với trục Ox là B, với trục Oy là A
Xét tam giác OAB vuông tại O ta có: \(\left\{{}\begin{matrix}OA=1\\OB=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow S_{OAB}=\dfrac{1}{2}\cdot1\cdot\dfrac{1}{2}=\dfrac{1}{4}\left(đvdt\right)\)
c) Gọi khoảng cách từ O đến (d) là đường cao OH của tam giác OAB ta có:
\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
\(\Rightarrow OH^2=\dfrac{OA^2OB^2}{OA^2+OB^2}=\dfrac{1^2\cdot\left(\dfrac{1}{2}\right)^2}{1^2+\left(\dfrac{1}{2}\right)^2}=\dfrac{1}{5}\)
\(\Rightarrow OH=\sqrt{\dfrac{1}{5}}=\dfrac{\sqrt{5}}{5}\)