Vẽ tam giác ABC, cho K là trung điểm của AB, J là một điểm trên BC sao cho BJ = 2/3 BC, KC cắt AJ tại I, chứng minh I là trung điểm của KC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2023
a: AM=6-2=6cm
AN=12-3=9cm
=>AM/AB=AN/AC
=>MN//BC
b: Xet ΔAKC có NI//KC
nên NI/KC=AI/AK
Xét ΔABK có MI//BK
nên MI/BK=AI/AK
=>NI/KC=MI/BK
c: NI/KC=MI/BK
KC=KB
=>NI=MI
=>I là tđ của MN
6 tháng 8 2023
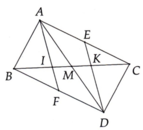
a: Xét ΔABD và ΔHBD có
BA=BH
góc ABD=góc HBD
BD chung
=>ΔABD=ΔHBD
b: Sửa đề: DK=DC
ΔABD=ΔHBD
=>góc BAD=góc BHD=90 độ
=>DH vuông góc BC
Xét ΔDAK vuông tại A và ΔDHC vuông tại H có
DA=DH
góc ADK=góc HDC
=>ΔDAK=ΔDHC
=>AK=HC và DK=DC
c: BA+AK=BK
BH+HC=BC
mà BA=BH và AK=HC
nên BK=BC
BK=BC
DK=DC
=>BD là trung trực của KC
=>B,D,I thẳng hàng
17 tháng 10 2021
a, Vì I là trung điểm AC và IN//AJ nên N là trung điểm CJ
b, Vì N là trung điểm CJ nên \(CN=NJ=BJ\left(=\dfrac{1}{3}BC\right)\)
Do đó J là trung điểm BN
Mà JO//IN (AJ//IN) nên O là trung điểm BI
29 tháng 1 2021
a) Ta có: ΔABC cân tại A(gt)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
⇒AM⊥BC(đpcm)
Ta có: M là trung điểm của BC(gt)
nên \(BM=MC=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí pytago vào ΔABM vuông tại M, ta được:
\(AB^2=AM^2+MB^2\)
\(\Leftrightarrow AM^2=AB^2-MB^2=5^2-3^2=16\)
hay AM=4(cm)
Vậy: AM=4cm
b) Ta có: AI+IB=AB(I nằm giữa A và B)
AJ+JC=AC(J nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và AI=AJ(gt)
nên BI=CJ(đpcm)
29 tháng 12 2023
Xét ΔABC có
AI,CK là các đường trung tuyến
AI cắt CK tại D
Do đó: D là trọng tâm của ΔABC
Xét ΔABC có
CK là đường trung tuyến
D là trọng tâm của ΔABC
Do đó: \(CD=\dfrac{2}{3}CK\)
Ta có: CD+DK=CK
=>\(DK=CK-\dfrac{2}{3}CK=\dfrac{1}{3}CK\)
=>CD=2KD
Lấy M sao cho C là trung điểm của AM
Xét ΔABM có
K,C lần lượt là trung điểm của AB,AM
=>KC là đường trung bình của ΔABM
=>KC//BM và \(KC=\dfrac{BM}{2}\)
Xét ΔABM có
BC là đường trung tuyến
\(BJ=\dfrac{2}{3}BC\)
Do đó: J là trọng tâm của ΔABM
=>AJ cắt BM tại trung điểm của N của BM
Xét ΔABM có
K,N lần lượt là trung điểm của BA,BM
=>KN là đường trung bình của ΔABM
=>KN//AM và KN=AM/2
KN=AM/2
AC=AM/2
Do đó: KN=AC
Xét tứ giác AKNC có
NK//AC
NK=AC
Do đó: AKNC là hình bình hành
=>AN cắt KC tại trung điểm của mỗi đường
=>I là trung điểm của KC(ĐPCM)