Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(\frac{-x+m}{x+2}=\frac{1-2x}{2}\) với x khác -2
\(\frac{-x+m}{x+2}=\frac{1-2x}{2}\Leftrightarrow\frac{-2x+2m}{2\left(x+2\right)}=\frac{\left(1-2x\right)\left(x+2\right)}{2\left(x+2\right)}\Leftrightarrow-2x+2m=\left(1-2x\right)\left(x+2\right)\Leftrightarrow-2x+2m=x-2x^2+2-4x\Leftrightarrow2x^2+x+2m-2=0\)
để đt d cắt đồ thị hàm số tại 2 điểm pt thì pt trên có 2 nghiệm phân biệt khác -2
làm tương tự như câu dưới......

Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
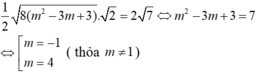
Chọn B.

a: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(m+1\right)x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x\left(m+1\right)=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=-\dfrac{3}{m+1}\end{matrix}\right.\)
vậy: \(A\left(-\dfrac{3}{m+1};0\right)\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m+1\right)\cdot x+3=0\left(m+1\right)+3=3\end{matrix}\right.\)
Vậy: B(0;3)
\(OA=\sqrt{\left(-\dfrac{3}{m+1}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{3}{m+1}\right)^2}=\left|\dfrac{3}{m+1}\right|\)
\(OB=\sqrt{\left(0-0\right)^2+\left(3-0\right)^2}=\sqrt{0+9}=3\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot3\cdot\dfrac{3}{\left|m+1\right|}=\dfrac{9}{2\left|m+1\right|}\)
Để \(S_{AOB}=9\) thì \(\dfrac{9}{2\left|m+1\right|}=9\)
=>2|m+1|=1
=>|m+1|=1/2
=>\(\left[{}\begin{matrix}m+1=\dfrac{1}{2}\\m+1=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{1}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)

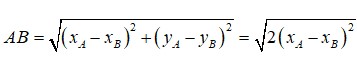
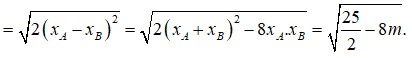
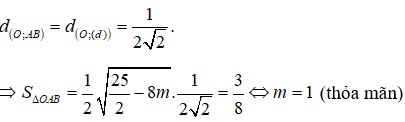



Tự vẽ hình nha, mình không biết vẽ hình trên này
* Cách vẽ: Vẽ trục tọa độ Oxy
Vẽ đường thẳng y = -3 (đường thẳng này đi qua điểm -3 trên trục Oy và song song với trục Ox)
Vẽ parabol \(y=mx^2\) nằm ở nửa mặt phẳng bờ Ox và âm của Oy (Khi đó parabol và đường thẳng y = -3 mới có điểm chung)
Gọi giao của Parabol với đường thẳng nói trên là A và B (A thuộc phần mặt phẳng có bờ là tia đối của tia Ox,Oy còn B là điểm còn lại đối xứng với A qua Oy)
AB cắt Oy tại H
* Bài làm:
Theo đề bài parabol và đường thẳng y = -3 cắt nhau tạo ra tam giác có diện tích là 10
\(\Rightarrow S_{OAB}=10\Leftrightarrow\frac{1}{2}\cdot\left|-3\right|\cdot AB=10\)
\(\Rightarrow AB=\frac{20}{3}\)\(\Rightarrow AH=BH=\frac{10}{3}\Rightarrow\left|x\right|=\frac{10}{3}\)
Khi đó tọa độ giao điểm của parabol và đường thẳng là \(\left(\frac{10}{3};-3\right);\left(-\frac{10}{3};-3\right)\)
Thay vào công thức parabol ta được: \(-3=\left(\frac{10}{3}\right)^2\cdot m\Rightarrow m=-\frac{27}{100}\)
Vậy \(m=-\frac{27}{100}\)