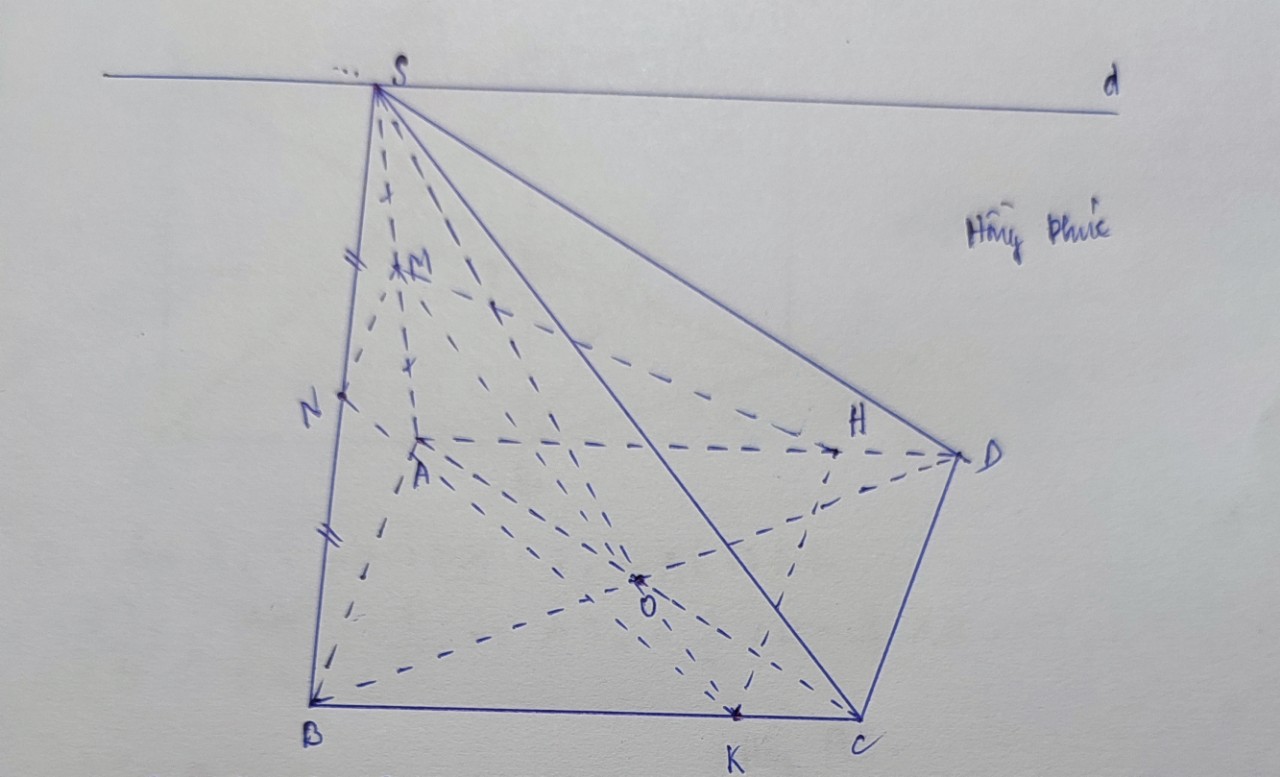
cho hình chóp s.abcd có đáy là hình bình hành . gọi g là trọng tâm của tam giác sad điểm m nằm trên đoạn dc sao cho dc=3dm
tìm giao tuyến (SAD) và (SBC)
tìm giao điểm K của đường thẳng BG và (SAC)
chứng minh rằng MG//(SBC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 10 2023
a: Chọn mp(SBD) có chứa BM
\(O\in BD\subset\left(SBD\right);O\in AC\subset\left(SAC\right)\)
Do đó: \(O\in\left(SBD\right)\cap\left(SAC\right)\)
mà \(S\in\left(SBD\right)\cap\left(SAC\right)\)
nên \(\left(SBD\right)\cap\left(SAC\right)=SO\)
Gọi E là giao điểm của SO với BM
=>E là giao điểm của BM với mp(SAC)
b: \(M\in SD\subset\left(SAD\right);M\in\left(MAC\right)\)
=>\(M\in\left(SAD\right)\cap\left(MAC\right)\)
mà \(A\in\left(MAC\right)\cap\left(SAD\right)\)
nên \(\left(MAC\right)\cap\left(SAD\right)=AM\)
CM
5 tháng 1 2018
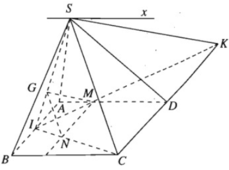
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
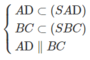
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
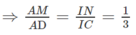
Mà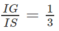 
(G là trọng tâm của ∆SAB) nên
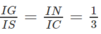⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
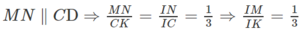
Ta có:
26 tháng 10 2023
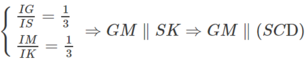
a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
b: Xét (SAD) và (SBC) có
AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
d: Trong mp(SAB), gọi I là giao điểm của AB với SM
\(I\in SM;I\in AB\subset\left(ABCD\right)\)
Do đó: I là giao điểm của SM với mp(ABCD)
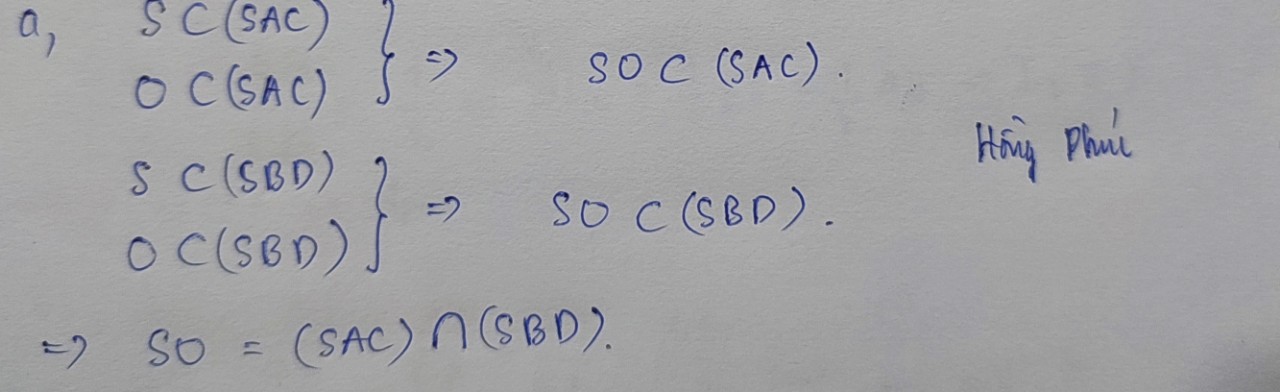
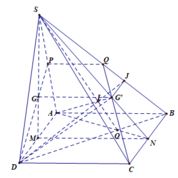
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
Mà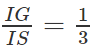
(G là trọng tâm của ∆SAB) nên
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
Ta có: