Cho hình chữ nhật ABCD. Vẽ AH vuông góc BD.
a) Chứng minh tam giác HAD đồng dạng tam giác CBD.
b) AH cắt CD tại M và cắt BC tại N. Chứng minh HA2 = HM.HN
(Không cần vẽ hình cũng được)
XIN CÁC CAO NHÂN GIÚP ĐỠ !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 3 2021
a) Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)
Do đó: ΔAHB\(\sim\)ΔBCD(g-g)
MH
13 tháng 5 2022
(Tự vẽ hình) Sửa đề: Phân giác của góc BCD cắt BD tại I
b) Do \(CI\) là phân giác nên ta có: \(\dfrac{IB}{ID}=\dfrac{BC}{CD}\)
Mặt khác: \(\Delta AHB\sim\Delta BCD\) (câu a)
\(\Rightarrow\dfrac{BC}{CD}=\dfrac{AH}{HB}\Rightarrow\dfrac{IB}{ID}=\dfrac{AH}{HB}\Rightarrow IB.HB=ID.AH\)
12 tháng 5 2023
a: Xét ΔBHI vuông tại H và ΔAKI vuông tại K có
góc BIH=góc AIK
=>ΔBHI đồng dạng vói ΔAKI
=>IB*IK=IA*IH
b: góc BHA=góc BKA=90 độ
=>BHKA nội tiếp
=>góc BAH=góc BKH
NA
17 tháng 4 2022
$#Shả$
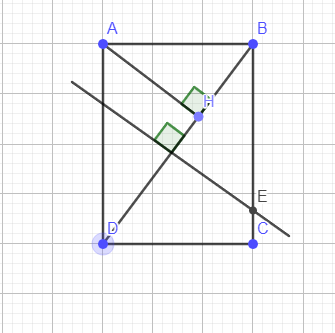
`a)` Xét `\triangleAHB` và `\triangleBCD` ta có `:`
`\hat{AHB}=\hat{BCD}=90^{o}`
`\hat{ABH}=\hat{BDC} ` (slt)
Vậy `\triangleAHB ` $\backsim$ `\triangleBCD` (g-g)
17 tháng 4 2022
a) △AHB và △BCD có: \(\widehat{AHB}=\widehat{BCD}=90^0\); \(\widehat{ABH}=\widehat{BDC}\) (AB//DC).
\(\Rightarrow\)△AHB∼△BCD (g-g).
b) △ABD có: \(BD^2=AD^2+AB^2\Rightarrow BD=\sqrt{AD^2+AB^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
△AHB∼△BCD \(\Rightarrow\dfrac{AH}{BC}=\dfrac{AB}{BD}=\dfrac{HB}{CD}\)
\(\Rightarrow\left[{}\begin{matrix}AH=\dfrac{AB.BC}{BD}=\dfrac{3.4}{5}=2,4\left(cm\right)\\HB=\dfrac{AB.CD}{BD}=\dfrac{3.3}{5}=1,8\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow S_{AHB}=\dfrac{1}{2}AH.HB=\dfrac{1}{2}.2,4.1,8=2,16\left(cm^2\right)\)
c) ABCD là hình chữ nhật, AC cắt BD tại O.
\(\Rightarrow\)O là trung điểm của AC và BD.
BD⊥DE tại D, CF⊥DE tại F. \(\Rightarrow\)BD//CF.
-△ODE có: IF//OD \(\Rightarrow\dfrac{IF}{OD}=\dfrac{EI}{EO}\).
-△OBE có: IC//OB \(\Rightarrow\dfrac{IC}{OB}=\dfrac{EI}{EO}=\dfrac{IF}{OD}\Rightarrow IC=IF\Rightarrow\)I là trung điểm CF.
Xét tam giác HAD và tam giác CBD có :
\(\hept{\begin{cases}\widehat{ADH}=\widehat{DBC}\left(\text{so le trong }\right)\\\widehat{AHD}=\widehat{DCB}\left(=90^{\text{o}}\right)\end{cases}}\)
=> \(\Delta HAD\approx\Delta CBD\left(g-g\right)\)
b) Xét tam giác BAH và tam giác DMH có
\(\hept{\begin{cases}\widehat{ABH}=\widehat{HDM}\left(\text{so le trong}\right)\\\widehat{AHB}=\widehat{MHD}\left(=90^{\text{o}}\right)\end{cases}}\)
=> \(\Delta BAH\approx\Delta DMH\left(g-g\right)\)
=> \(\frac{BH}{DH}=\frac{AH}{MH}\)(1)
Tương tự \(\Delta ADH\approx\Delta NBH\left(g-g\right)\)
=> \(\frac{BH}{DH}=\frac{NH}{AH}\left(2\right)\)
Từ (1)(2) => \(\frac{AH}{MH}=\frac{NH}{AH}\Rightarrow AH^2=NH.MH\)
CHƠI FREE FIRE À