Cho tam giác ABC cân ở A, AB = AC = 6cm, BH = 5cm tinh dien tich tam giac ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
P
Phong
CTVHS
18 tháng 10 2023
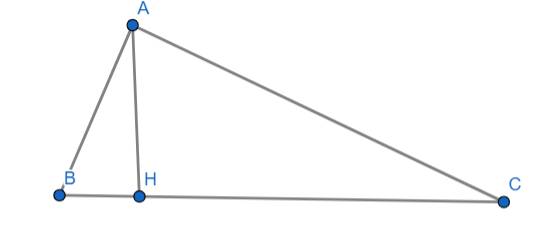
Xét tam giác vuông ABC vuông tại A có đường cao AH là:
\(AC^2=HC\cdot BC\)
\(\Rightarrow AC^2=\left(BC-HB\right)\cdot BC\)
\(\Rightarrow6^2=\left(BC-5\right)\cdot BC\)
\(\Rightarrow BC^2-5BC-36=0\)
\(\Rightarrow\left[{}\begin{matrix}BC=9\left(cm\right)\left(tm\right)\\BC=-4\left(cm\right)\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow AB=\sqrt{BC\cdot BH}=\sqrt{9\cdot5}=3\sqrt{5}\left(cm\right)\)
\(\Rightarrow AH=\dfrac{AB^2\cdot AC^2}{AB^2+AC^2}=\dfrac{6^2\cdot\left(3\sqrt{5}\right)^2}{6^2+\left(3\sqrt{5}\right)^2}=20\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot9\cdot20=90\left(cm^2\right)\)
8 tháng 1 2019
IQ vô cực mới có thể giải... Rất tiết mình ko trả lời đc
21 tháng 10 2017
Hình 1 nếu giữ nguyên AB và thêm AC 2 cm
Phần được tô là diện tích tăng thêm .
Độ dài AB LÀ :
6 : 2 = 3 ( cm )
29 tháng 7 2018
a, Xét 2 tam giác ADE và ACB
Góc A chung
AD/AC=AE/AB =1/2
=> Tam giác ADE đồng dạng tam giác ACB
b, tA CÓ : SADE / SACB = (AD/AC)2 = 1/4
=> SADE = 1/4 * SACB = 1/4 *S
Xét tam giác vuông ABH vuông tại H ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}\)
\(\Rightarrow AH=\sqrt{6^2-5^2}=\sqrt{11}\left(cm\right)\)
Mà tam giác ABC cân tại A nên \(BC=2BH=2\cdot5=10\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot\sqrt{11}=5\sqrt{11}\left(cm^2\right)\)