ML
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ML
1
H9
HT.Phong (9A5)
CTVHS
18 tháng 10 2023
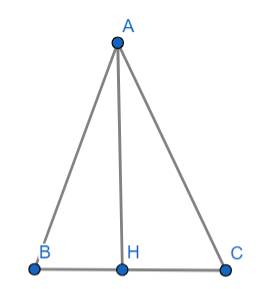
Xét tam giác vuông ABH vuông tại H ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}\)
\(\Rightarrow AH=\sqrt{6^2-5^2}=\sqrt{11}\left(cm\right)\)
Mà tam giác ABC cân tại A nên \(BC=2BH=2\cdot5=10\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot\sqrt{11}=5\sqrt{11}\left(cm^2\right)\)
LM
1 tháng 6 2017
áp dụng hệ thức lượng trong tam giác ABC
AN2=BH.BC
=>BC=AB2:BH=25
từ đó áp dụng pytago tính AC=20
lại áp dụng hệ thức lượng ta có;
AH.BC=AB.AC
=>AH=(AB.AC):BC=12
trong tam giác vuông trung tuyễn ứng vs cạnh huyền có số đo = nửa cạnh huyền
=> AM=12,5
=> HM=3,5 theo pytago
=> SAMH=1phần 2 AH.HM=21
PV
0
Xét tam giác vuông ABC vuông tại A có đường cao AH là:
\(AC^2=HC\cdot BC\)
\(\Rightarrow AC^2=\left(BC-HB\right)\cdot BC\)
\(\Rightarrow6^2=\left(BC-5\right)\cdot BC\)
\(\Rightarrow BC^2-5BC-36=0\)
\(\Rightarrow\left[{}\begin{matrix}BC=9\left(cm\right)\left(tm\right)\\BC=-4\left(cm\right)\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow AB=\sqrt{BC\cdot BH}=\sqrt{9\cdot5}=3\sqrt{5}\left(cm\right)\)
\(\Rightarrow AH=\dfrac{AB^2\cdot AC^2}{AB^2+AC^2}=\dfrac{6^2\cdot\left(3\sqrt{5}\right)^2}{6^2+\left(3\sqrt{5}\right)^2}=20\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot9\cdot20=90\left(cm^2\right)\)