Chứng minh rằng
a) (3693 - 2193) ⋮1350
b) (3723 - 1283) ⋮1000
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
2
Những câu hỏi liên quan
HL
0
PT
1
CM
3 tháng 9 2018
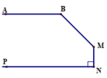
Qua điểm M kẻ tia Mx // NP (3).
Khi đó
| N M x ^ = 90 0 M N ⊥ N P |
Xét A B M ^ + x M B ^ = 135 0 + 45 0 = 180 0 => AB // Mx (có cặp góc trong cùng phía bù nhau) (4).
Từ (3) và (4) suy ra AB // NP (đpcm).
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 1 2022
\(bx^2=ay^2\Rightarrow\dfrac{x^2}{a}=\dfrac{y^2}{b}=\dfrac{x^2+y^2}{a+b}=\dfrac{1}{a+b}\)
\(\Rightarrow\left(\dfrac{x^2}{a}\right)^{1000}=\left(\dfrac{y^2}{b}\right)^{1000}=\left(\dfrac{1}{a+b}\right)^{1000}\)
\(\Rightarrow\dfrac{x^{2000}}{a^{1000}}=\dfrac{y^{2000}}{b^{1000}}=\dfrac{1}{\left(a+b\right)^{1000}}\)
\(\Rightarrow\dfrac{x^{2000}}{a^{1000}}+\dfrac{y^{2000}}{b^{1000}}=\dfrac{1}{\left(a+b\right)^{1000}}+\dfrac{1}{\left(a+b\right)^{1000}}=\dfrac{2}{\left(a+b\right)^{1000}}\)
26 tháng 7 2022
a: \(P=3^3\left(123^3-73^3\right)\)
\(=3\cdot9\cdot\left(123-73\right)\cdot A=1350\cdot A\cdot3⋮1350\)
b: \(=4^3\left(93^4+32^4\right)\)
\(=4^3\left(93+32\right)\cdot A=125\cdot64\cdot A=8000\cdot A⋮8000\)
16 tháng 9 2023
Tổng A có 1000 số hạng
A>(1001/1000^2+1000)*1000=1001*1000/1000*(1000+1)=1
A<(1001/1000^2)*1000=1001/1000=1+1/1000<1
Vậy 1<A<2 nên 1<A^2<4
8 tháng 7 2018
Ta có:\(B=3-10x^2-4xy-4y^2\)
\(=3-9x^2-x^2-4xy-4y^2\)
\(=3-9x^2-\left(x^2+4xy+4y^2\right)\)
\(=3-\left(3x\right)^2-\left(x+2y\right)^2\)
Vì \(\hept{\begin{cases}\left(3x\right)^2\ge0\\\left(x+2y\right)^2\ge0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}-\left(3x\right)^2\le0\\-\left(x+2y\right)^2\le0\end{cases}}\)
\(\Rightarrow B=3-\left(3x\right)^2-\left(x+2y\right)^2\le3-0-0=3\)
Nên GTLN của B là 3 đạt được khi \(\hept{\begin{cases}3x=0\\x+2y=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\2y=-x\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\2y=0\end{cases}\Leftrightarrow}x=y=0\)
Dùng HĐT \(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\) là ra thôi bạn.
a) \(VT=\left(369-219\right)\left(369^2+369.219+219^2\right)\)
\(=150\left(369^2+369.219+219^2\right)\)
Ta chỉ cần chứng minh \(P=369^2+369.219+219^2⋮9\). Đến đây ta lại nhớ tới 1 bổ đề về số chính phương như sau: Nếu một số chính phương mà chia hết cho 3 thì nó cũng chia hết cho 9. Theo bổ đề này và do \(369,219⋮3\) nên dễ dàng suy ra \(P⋮9\). Suy ra đpcm.
Câu b làm tương tự.
nó làm đúng vì tôi cũng không biết