
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C O 1 1
Giải:
Xét \(\Delta BOC\) có: \(\widehat{BOC}+\widehat{B_1}+\widehat{C_1}=180^o\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=50^o\left(\widehat{BOC}=130^o\right)\)
\(\Rightarrow2\left(\widehat{B_1}+\widehat{C_1}\right)=100^o\)
\(\Rightarrow2.\widehat{B_1}+2.\widehat{C_1}=100^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=100^o\)
Xét \(\Delta ABC\) có: \(\widehat{BAC}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{BAC}=80^o\)
Vậy \(\widehat{BAC}=80^o\)

Bài 2:
a: \(\left|x\right|=-x\)
nên x<=0
b: \(\left|x\right|>x\)
=>x<0

c, \(\left(7-3x\right)\left(2x+1\right)=0\)
=> \(7-3x=0\) hoặc \(2x+1=0\)
\(3x=7-0\) hoặc \(2x=0-1\)
\(3x=7\) hoặc \(2x=-1\)
\(x=7:3\) hoặc \(x=-1:2\)
\(x=\dfrac{7}{3}\) hoặc \(x=-0,5\)
Vậy, \(x\in\left\{\dfrac{7}{3};-0,5\right\}\)

Với mọi x thuộc R Có (x^2-9)^2 \(\ge\) 0
[y-4] \(\ge\) 0
Suy ra (x^2-9)^2+[y-4] - 1 \(\ge\) -1
Xét A=-1 khi và chỉ khi (x^2-9)^2 và [y-4] đều bằng 0
Tự tính ra
Xin lỗi nhưng vì không biết nên mình phải dùng [ ] thay cho GTTĐ nhé
Xin lỗi nhiều tại mình o tìm được kí hiệu đó

Từ \(\dfrac{ab}{a+b}=\dfrac{bc}{b+c}=\dfrac{ca}{c+a}\)
\(\Rightarrow\dfrac{a+b}{ab}=\dfrac{b+c}{bc}=\dfrac{c+a}{ca}\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{c}+\dfrac{1}{a}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{b}+\dfrac{1}{c}\\\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{c}+\dfrac{1}{a}\\\dfrac{1}{c}+\dfrac{1}{a}=\dfrac{1}{a}+\dfrac{1}{b}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{a}=\dfrac{1}{c}\\\dfrac{1}{b}=\dfrac{1}{a}\\\dfrac{1}{c}=\dfrac{1}{b}\end{matrix}\right.\)\(\Rightarrow\dfrac{1}{a}=\dfrac{1}{b}=\dfrac{1}{c}\Rightarrow a=b=c\)
Khi đó \(P=\dfrac{ab^2+bc^2+ca^2}{a^3+b^3+c^3}=\dfrac{3a^3}{3a^3}=1\)
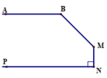
Qua điểm M kẻ tia Mx // NP (3).
Khi đó
Xét A B M ^ + x M B ^ = 135 0 + 45 0 = 180 0 => AB // Mx (có cặp góc trong cùng phía bù nhau) (4).
Từ (3) và (4) suy ra AB // NP (đpcm).