tìm hai số tự nhiên liên tiếp,biết rằng hiệu các bình phương của chúng bằng 31
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AA
1
20 tháng 6 2017
Gọi số bé nhất trong 2 số đó là a (a thuộc N)
=> Số còn lại là a+1
Vì hiệu bình phương của chúng bằng 40 nên ta có phương trình sau:
(a+1)2 - a2 = 40
<=> a2 + 2a + 1 - a2 = 40
2a + 1 = 40
a = 19,5 (k thoả mãn a thuộc N)
Vậy, không tìm được 2 số thoả mãn đề bài
Bạn thử xem lại đề bài xem, vì 2 số tn liên tiếp sẽ 1 lẻ 1 chẵn, bình phương lên cũng 1 lẻ 1 chẵn, vậy hiệu phải là số lẻ chứ
BT
1
DD
6 tháng 8 2015
Gọi 2 số lẻ liên tiếp là a^2,(a+2)^2.
Ta có (a+2)^2-a^2=a^2+4a+4-a^2=4a+4=56.
=>4a=52=> a=13. Vậy 2 số lẻ liên tiếp đó là 13,15
N
3
NX
26 tháng 8 2023
Gọi 2 số tự nhiên đó là: a; a-1\(\left(a\inℕ^∗\right)\)
Theo đề bài ta có:
\(a^2-\left(a-1\right)^2=31\)
\(\Leftrightarrow a^2-\left(a^2-2a+1\right)=31\)
\(\Leftrightarrow a^2-a^2+2a-1=31\)
\(\Leftrightarrow2a=31+1\)
\(\Leftrightarrow a=\dfrac{32}{2}=16\Rightarrow a-1=16=16-1=15\)
Vậy hai số đó là: \(15;16\)
28 tháng 8 2023
Gọi hai số tự nhiên đó là a , a - 1 (a N*)
Theo đề, ta có :
Vậy : Hai số đó là 15; 16
MH
12 tháng 6 2015
Bài 2 :
a+b=5 <=> ( a+b)2=52
<=> a2+ab+b2=25
Hay : a2+1+b2=25
<=> a2+b2=24
Bài 4 : Gọi 2 số tự nhiên lẻ liên tiếp lần lượt là : a, a+2 ( a lẻ , a thuộc N 0
Theo bài ra , ta có : ( a+2)2-a2= 56
<=> a2+4a+4-a2=56
<=> 4a=56-4
<=> 4a=52
<=> a=13
Vậy 2 số tự nhiên lẻ liên tiếp là : 13; 15
NT
0
26 tháng 5 2015
Gọi 2 số cần tìm là a và b (là số tự nhiên)
Theo bài ra ta có: a-b=2
a2-b2=36
=>(a-b)(a+b)=36
=>2(a+b)=36
=>a+b=18
=>a=(18+2):2=10
b=10-2=8
Vậy 2 số cần tìm là 10 và 8
LT
29 tháng 7 2018
À, bài 1 mk biết làm rồi nên mn chie cần trả lời câu thứ hai thui. Cảm ơn.
LT
29 tháng 7 2018
Cho mk xin lỗi mk biết làm bài 2 chứ không biết làm bài 1. Xin lỗi mn.
CM
7 tháng 2 2019
Đáp án A
Gọi số thứ nhất là a; a ∈ N, số thứ hai là b; b ∈ N Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:
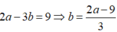
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:
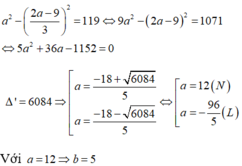
Vậy số lớn hơn là 12.
Gọi hai số đó có dạng: \(x,x+1\) (\(x\in N\))
Hiệu các bình phương của chúng là 31 nên ta có: \(\left(x+1\right)^2-x^2=31\) (1)
Giải phương trình (1) ta có:
\(\left(x+1\right)^2-x^2=31\)
\(\Leftrightarrow x^2-x^2+2x+1=31\)
\(\Leftrightarrow2x+1=31\)
\(\Leftrightarrow2x=30\)
\(\Leftrightarrow x=15\)
Vậy hai số đó là: \(15,16\)