Tìm n ∈ N, biết: 2n + 4.2n = 255.25
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
15 tháng 2 2022
- 2k9isthebest
- 28/07/2021
Đáp án:
12.2n+4.2n=9.5n12.2n+4.2n=9.5n
2n.(12+4) =9.5n2n.(12+4) =9.5n
2n.92 =9.5n2n.92 =9.5n
2n =9:92.5n2n =9:92.5n
2n =2.5n2n =2.5n
2n:5n =22n:5n =2
(25)n =2(25)n =2
Mà (25)n≠2(25)n≠2 nên không có giá trị nào của n thỏa mãn
Vậy n∈{∅}
T.I.C.K NHÉ
1
4
LP
0
TC
2
21 tháng 3 2021
Ta có : \(C^k_{2n+1}=C^{2n+1-k}_{2n+1}\)
\(\Rightarrow2VT=C^1_{2n+1}+C^2_{2n+1}+...+C^{2n}_{2n+1}=2^{21}-2\)
\(\Leftrightarrow2^{2n+1}-C^0_{2n+1}-C^{2n+1}_{2n+1}=2^{21}-2\)
\(\Leftrightarrow2n+1=21\Leftrightarrow n=10\)
21 tháng 3 2021
\(\sum\limits^{2n+1}_{k=0}C^k_{2n+1}=\left(1+1\right)^{2n+1}=2^{2n+1}\)
Lại có \(C^0_{2n+1}+C^1_{2n+1}+...+C^n_{2n+1}=C^{2n+1}_{2n+1}+C^{2n}_{2n+1}+...+C^{n+1}_{2n+1}\)
\(\Rightarrow C^0_{2n+1}+C^1_{2n+1}+...C^n_{2n+1}=\dfrac{2^{2n+1}}{2}\)
\(\Leftrightarrow2^{20}-1=2^{2n}-C^0_{2n+1}\)
\(\Leftrightarrow2^{20}-1=2^{2n}-1\)
\(\Leftrightarrow2n=20\)
\(\Leftrightarrow n=10\)
T
19 tháng 8 2023
a.(2^2 : 4) . 2^n = 4
=>(4:4) . 2^n = 4
=>2^n = 4
=>2^n = 2^2
=>n=2
b.2.16 >_ 2^n > 4
=>32 >_ 2^n > 2^2
=>2^5 >_ 2^n > 2^2
=>n={3;4;5}
HQ
Hà Quang Minh
Giáo viên
19 tháng 8 2023
\(a,\left(2^2:4\right)\cdot2^n=4\\ \Leftrightarrow2^n=2^2\\ \Leftrightarrow n=2\)
\(b,2\cdot16\ge2^n>4\\ \Leftrightarrow2^5\ge2^n>2^2\\ \Rightarrow2< n\le5\\ \Leftrightarrow n\in\left\{3;4;5\right\}\)
27 tháng 12 2016
Theo bài ra ta có:
2n + 8 chia hết cho 2n + 1
=> ( 2n + 1 ) + 7 chia hết cho 2n + 1
=> 7 chia hết cho 2n + 1
=> 2n + 1 thuộc { 1 ; 7 }
=> 2n thuộc { 0 ; 6 }
=> n thuộc { 0 ; 3 }
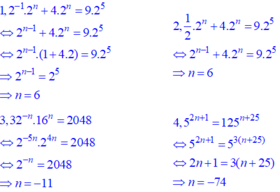
2^n+4.2^n=255.32
2^n+4.2^n=8160
2^n.1+4.2^n=8160
2^n.( 1+4 )= 8160
2^n.5=8160
2^n=8160:5
2^n=1632
Mk chỉ làm đc đến đó thoi còn lại bạn tự suy nghĩ nhé