Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số \(0;\;1;\;\sqrt 2 ;\; - \sqrt 2 \). Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) với vecto \(\overrightarrow a = \overrightarrow {OA} \). Viết đẳng thức thể hiện mối quan hệ giữa hai vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì P là hình chiếu vuông góc của M trên Ox nên điểm P biểu diễn hoành độ của điểm M là số \({x_o}\)
Ta có: vectơ \(\overrightarrow {OP} \) cùng phương, cùng hướng với \(\overrightarrow i \) và \(\left| {\overrightarrow {OP} } \right| = {x_o} = {x_o}.\left| {\overrightarrow i } \right|\)
\( \Rightarrow \overrightarrow {OP} = {x_o}.\;\overrightarrow i \).
b) Vì Q là hình chiếu vuông góc của M trên Oy nên điểm Q biểu diễn tung độ của điểm M là số \({y_o}\)
Ta có: vectơ \(\overrightarrow {OQ} \) cùng phương, cùng hướng với \(\overrightarrow j \) và \(\left| {\overrightarrow {OQ} } \right| = {y_o} = {y_o}.\left| {\overrightarrow j } \right|\)
\( \Rightarrow \overrightarrow {OQ} = {y_o}.\;\overrightarrow j \).
c) Ta có: \(\overrightarrow {OM} = OM\).
Mà \(O{M^2} = O{P^2} + M{P^2} = O{P^2} + O{Q^2} = {x_o}^2 + {y_o}^2\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt {{x_o}^2 + {y_o}^2} \)
d) Ta có: Tứ giác OPMQ là hình chữ nhật, cũng là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {OP} + \overrightarrow {OQ} \)
\( \Rightarrow \overrightarrow {OM} = {x_o}.\;\overrightarrow i + {y_o}.\;\overrightarrow j \)

Dễ thấy:
vectơ \(\overrightarrow {OM} \) cùng hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {OM} } \right| = 4 = 4\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {OM} = 4\,.\,\overrightarrow i \)
Tương tự, vectơ \(\overrightarrow {ON} \) ngược hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {ON} } \right| = \frac{3}{2} = \frac{3}{2}\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {ON} = - \frac{3}{2}\,.\,\overrightarrow i \)

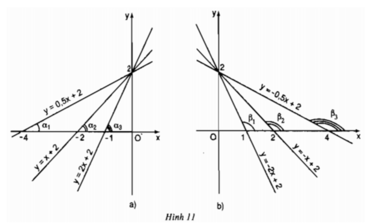
a) Ta có: α 1 < α 2 < α 3 và các giá trị tương ứng của hệ số a trong các hàm số :
0,5 < 1 < 2
Nhận xét: Khi hệ số a dương (a > 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90o
b) Ta có: β 1 < β 2 < β 3 và các giá trị tương ứng của hệ số a trong các hàm số
-2 < -1 < -0,5
Nhận xét : Khi hệ số a âm (a < 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180o

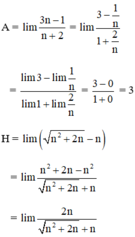
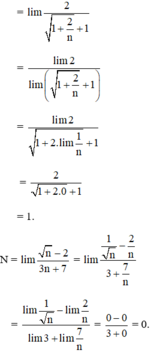
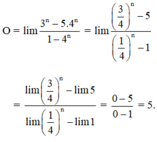
Khi thay đổi chữ số 1530 bởi các biểu thức giới hạn tương ứng ta được chữ HOAN là tên các bạn học sinh đã cho.

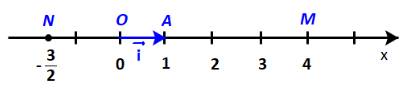
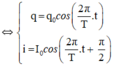
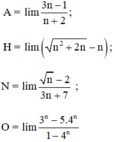
Dễ thấy:
Vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \)có cùng giá nên chúng cùng phương.
Mà vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \)cùng nằm trên tia OM nên chúng cùng chiều
Vậy vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \)cùng hướng.
Ngoài ra, \(\left| {\overrightarrow {OM} } \right| = OM = \sqrt 2 \) và \(\left| {\overrightarrow {OA} } \right| = OA = 1\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt 2 .\left| {\overrightarrow {OA} } \right|\)
Ta kết luận \(\overrightarrow {OM} = \sqrt 2 .\overrightarrow {OA} \).