Cho hàm số \(y = \frac{1}{x}\) và ba điểm \(M\left( { - 1; - 1} \right),N\left( {0;2} \right),P\left( {2;1} \right)\). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}{x^2} - \frac{1}{2}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {{x^2} - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{2}\left( {x + 1} \right) = \frac{1}{2}\left( {1 + 1} \right) = 1\end{array}\)
b) Phương trình đường thẳng \(d\) đi qua điểm \(M\left( {1;\frac{1}{2}} \right)\) và có hệ số góc bằng \(k = f'\left( 1 \right) = 1\) là: \(y - \frac{1}{2} = 1\left( {x - 1} \right) \Leftrightarrow y = x - 1 + \frac{1}{2} \Leftrightarrow y = x - \frac{1}{2}\).

Đường thẳng \(d\) cắt đồ thị hàm số \(\left( C \right)\) tại duy nhất điểm \(M\left( {1;\frac{1}{2}} \right)\).

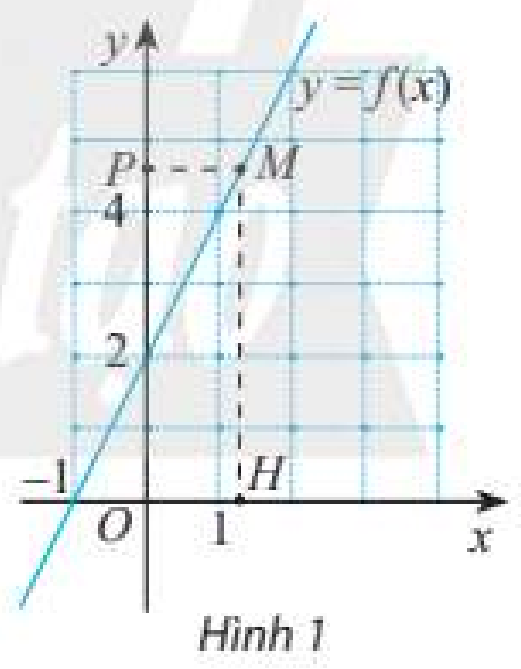
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).

Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2

- Với \(x< 3\Rightarrow f'\left(x\right)=6x^2-6\left(m+1\right)x+6m=6\left(x-1\right)\left(x-m\right)\)
\(f'\left(x\right)=0\Rightarrow6\left(x-1\right)\left(x-m\right)=0\left(1\right)\Rightarrow\left[{}\begin{matrix}x=1\\x=m\end{matrix}\right.\) có tối đa 2 cực trị khi \(x< 3\)
- Với \(x>3\Rightarrow f'\left(x\right)=n\) là hằng số \(\Rightarrow f\left(x\right)\) ko có cực trị khi \(x>3\)
\(\Rightarrow\) Hàm có đúng 3 điểm cực trị khi và chỉ khi nó đồng thời thỏa mãn:
ĐK1: \(f'\left(x\right)=0\) có 2 nghiệm pb khi \(x< 3\Rightarrow\left\{{}\begin{matrix}m< 3\\m\ne1\end{matrix}\right.\)
ĐK2: \(x=3\) là 1 cực trị của hàm số
\(\Rightarrow f\left(x\right)\) liên tục tại \(x=3\) đồng thời đạo hàm đổi dấu khi đi qua \(x=3\)
\(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)\Leftrightarrow3n+46=25-9m\Rightarrow n=-3m-7\) (2)
Mặt khác do 2 nghiệm của (1) đều nhỏ hơn 3 \(\Rightarrow\) tại lân cận trái của \(x=3\) đạo hàm luôn có dấu dương
\(\Rightarrow\) Để đạo hàm đổi dấu khi đi qua \(x=3\) thì \(f'\left(3^+\right)=n< 0\)
Thế vào (2) \(\Rightarrow-3m-7< 0\Rightarrow m>-\dfrac{7}{3}\)
\(\Rightarrow-\dfrac{7}{3}< m< 3\Rightarrow\sum m=0\)

Hàm số đã cho có 3 điểm cực trị \(\Leftrightarrow y'=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3-2\left(3m+1\right)x=0\) có 3 nghiệm phân biệt \(\Leftrightarrow m>-\frac{1}{3}\) (1)
Khi đó 3 điểm cực trị của đồ thị là \(A\left(0;2m+2\right);B\left(-\sqrt{6m+2};-9m^2-4m+1\right);C\left(\sqrt{6m+2};-9m^2-4m+1\right)\)
Rõ ràng tam giác ABC cân tại A và trung tuyến kẻ từ A thuộc Oy. Do đó O là trọng tâm của tam giác ABC \(\Leftrightarrow y_A+2y_B=0\)
Hay \(2m+2+2\left(-9m^2-4m+1\right)=0\Leftrightarrow9m^2+3m-2=0\)
Suy ra \(m=-\frac{2}{3}\) hoặc \(m=\frac{1}{3}\)
Kết hợp với (1) suy ra giá trị của m là \(m=\frac{1}{3}\)

y x 1 -2/5 0 y=-2x/5
- \(y\left(-5\right)=\frac{-2.\left(-5\right)}{5}=2\Rightarrow N\in\left(d\right)\)
- \(y\left(0\right)=\frac{-2.0}{5}=0\ne3\Rightarrow M\notin\left(d\right)\)
- \(y\left(3\right)=\frac{-2.3}{5}=\frac{-6}{5}=-1\frac{1}{5}\Rightarrow P\in\left(d\right)\)

\(y'=2x^2-6\left(m+1\right)x+9\)
Để hàm số có cực đại, cực tiểu
\(\Delta'=9\left(m+1\right)^2=3.9>0\)
\(=\left(m+1\right)^2-3>0\)
\(\Leftrightarrow m\in\left(-\infty;-1-\sqrt{3}\right)\cup\left(-1+\sqrt{3};+\infty\right)\)
Ta có : \(y=\left(\frac{1}{3}x-\frac{m+1}{3}\right)\left(3x^2-6\left(m+1\right)x+9\right)-2\left(m^2+2m-2\right)x+4m+1\)
Gọi tọa độ điểm cực đại và cực tiểu là \(\left(x_1;y_1\right)\) và \(\left(x_2;y_2\right)\)
=> \(y_1=-2\left(m^2+2m-2\right)x_1+4m+1\)
\(y_2=-2\left(m^2+2m-2\right)x_2+4m+1\)
Vậy đường thẳng đi qua 2 điểm cực đại và cực tiểu là
\(y=-2\left(m^2+2m-2\right)x+4m+1\)
Vì 2 điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng \(y=\frac{1}{2}x\) ta có điều kiện cần là :
\(\left[-2\left(m^2+2m-2\right)\right]\frac{1}{2}=-1\)
\(\Leftrightarrow m^2+2m-2=1\)
\(\Leftrightarrow m^2+2m-3=0\)
\(\Leftrightarrow\begin{cases}m=1\\m=-3\end{cases}\)
Theo định lí Viet ta có \(\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=3\end{cases}\)
Khi m =1 => phương trình đường thẳng đi qua 2 điểm cực đại và cực tiểu là
\(y=-2x+5\)
Tọa độ trung điểm cực đại và cực tiểu là :
\(\begin{cases}\frac{x_1+x_2}{2}=\frac{4}{2}=2\\\frac{y_1+y_2}{2}=\frac{-2\left(x_1+x_2\right)+10}{2}=1\end{cases}\)
Tọa độ trung điểm cực đại và cực tiểu là (2;1) thuộc đường thẳng \(y=\frac{1}{2}x\Rightarrow m=1\) thỏa mãn
Khi m=-3 phương trình đường thẳng đi qua 2 điểm cực đại và cực tiểu là y=-2x-11
(làm tương tự cách như trên)

a) Với \(x\in\left[0;1\right]\) => x - 2 < 0 => |x - 2| = - (x -2)
Khi đó, \(f\left(x\right)=2\left(m-1\right)x+\frac{m\left(x-2\right)}{-\left(x-2\right)}=2\left(m-1\right)x-m\)
Để f(x) < 0 với mọi \(x\in\left[0;1\right]\) <=> \(2\left(m-1\right)x-m<0\) (*) với mọi \(x\in\left[0;1\right]\)
+) Xét m - 1 > 0 <=> m > 1
(*) <=> \(x<\frac{m}{2\left(m-1\right)}\). Để (*) đúng với mọi \(x\in\left[0;1\right]\) <=> \(\frac{m}{2\left(m-1\right)}\ge1\) <=> 2(m -1) \(\le\)m <=> m \(\le\) 2 <=> m \(\le\) 2
Kết hợp điều kiện m > 1 =>1 < m \(\le\) 2
+) Xét m = 1 thì (*) <=> -1 < 0 luôn đúng => m =1 thỏa mãn
+) Xét m - 1 < 0 <=> m < 1
(*) <=> \(x>\frac{m}{2\left(m-1\right)}\). Để (*) đúng với mọi \(x\in\left[0;1\right]\) <=> \(\frac{m}{2\left(m-1\right)}\le0\) <=> m \(\ge\) 0 (do m< 1 ). Kết hợp m < 1 => 0 \(\le\) m < 1
Kết hợp các trường hợp : Với 0 \(\le\)m \(\le\) 2 thì .....
b) Hoành độ giao điểm của đò thị hàm số với Ox là nghiệm của Phương trình : \(2\left(m-1\right)x+\frac{m\left(x-2\right)}{\left|x-2\right|}=0\) (1)
Đồ thị hàm số cắt Ox tại điểm có hoành độ xo thuộc (1;2) => xo < 2 => |xo - 2| = - (xo - 2)
xo là nghiệm của (1) <=> \(2\left(m-1\right)x_o+\frac{m\left(x_o-2\right)}{\left|x_o-2\right|}=0\) <=> \(2\left(m-1\right)x_o-m=0\)
+) Xét m \(\ne\) 1 thì (2)<=> \(x_o=\frac{m}{2\left(m-1\right)}\). Vì 1 < xo < 2 nên \(1<\frac{m}{2\left(m-1\right)}<2\) <=> \(\begin{cases}\frac{m}{2\left(m-1\right)}-1>0\\\frac{m}{2\left(m-1\right)}-2<0\end{cases}\) <=> \(\begin{cases}\frac{-m+2}{2\left(m-1\right)}>0\left(a\right)\\\frac{-3m+4}{2\left(m-1\right)}<0\left(b\right)\end{cases}\)
Giải (a) <=> 1 < m < 2
Giải (b) <=> m < 1 hoặc m > 4/3
Kết hợp nghiệm của (a) và (b) => 4/3 < m < 2
+) Xét m = 1 thì (2) <=> -1 = 0 Vô lí
Vậy Với 4/3 < m < 2 thì đồ thị hàm số cắt Ox tại điểm thuộc (1;2)

Lời giải:
1.PT hoành độ giao điểm:
$x^2-mx-4=0(*)$
Khi $m=3$ thì pt trở thành: $x^2-3x-4=0$
$\Leftrightarrow (x+1)(x-4)=0$
$\Rightarrow x=-1$ hoặc $x=4$
Với $x=-1$ thì $y=(-1)^2=1$. Giao điểm thứ nhất là $(-1;1)$
Với $x=4$ thì $y=4^2=16$. Giao điểm thứ hai là $(4;16)$
2.
$\Delta (*)=m^2+16>0$ với mọi $m\in\mathbb{R}$ nên PT $(*)$ luôn có 2 nghiệm phân biệt $x_1,x_2$, đồng nghĩa với việc 2 ĐTHS luôn cắt nhau tại 2 điểm phân biệt $A(x_1,y_1); B(x_2,y_2)$
Áp dụng định lý Viet:
$x_1+x_2=m$ và $x_1x_2=-4$
Khi đó:
$y_1^2+y_2^2=49$
$\Leftrightarrow (mx_1+4)^2+(mx_2+4)^2=49$
$\Leftrightarrow m^2(x_1^2+x_2^2)+8m(x_1+x_2)=17$
$\Leftrightarrow m^2[(x_1+x_2)^2-2x_1x_2]+8m(x_1+x_2)=17$
$\Leftrightarrow m^2(m^2+8)+8m^2=17$
$\Leftrightarrow m^4+16m^2-17=0$
$\Leftrightarrow (m^2-1)(m^2+17)=0$
$\Rightarrow m^2=1$
$\Leftrightarrow m=\pm 1$

Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Ta thấy \({x_N} = 0\)=> Điểm N không thuộc đồ thị.
Thay \({x_M} = - 1\) vào ta được: \(y = \frac{1}{{ - 1}} = - 1\)=> Điểm M thuộc đồ thị.
Thay \({x_P} = 2\) vào ta được: \(y = \frac{1}{2} \ne {y_P}\)=> Điểm P không thuộc đồ thị.