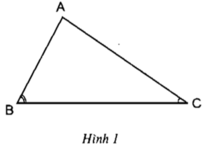
Em hãy dựng tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh AC của tam giác.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


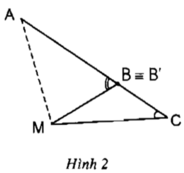
Ta nhận thấy 2 hình bằng nhau (chồng lên nhau vì vừa khít)

Ta có: góc AB’M là góc ngoài của tam giác MB’C
Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C

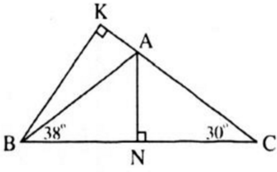
Kẻ BK ⊥ AC (K ∈ AC).
Trong tam giác vuông BKC có:
∠ K B C = 9 ° o – 30 ° = 60 ° = > ∠ K B A = 60 ° – 38 ° = 22 °
BC = 11 (cm) => BK = 5,5 (cm) ( tính chất cạnh đối diện góc 30° trong tam giác vuông bằng nửa cạnh huyền )
Xét tam giác ABK vuông tại K:
![]()
![]()
Xét tam giác ANB vuông tại N:
![]()
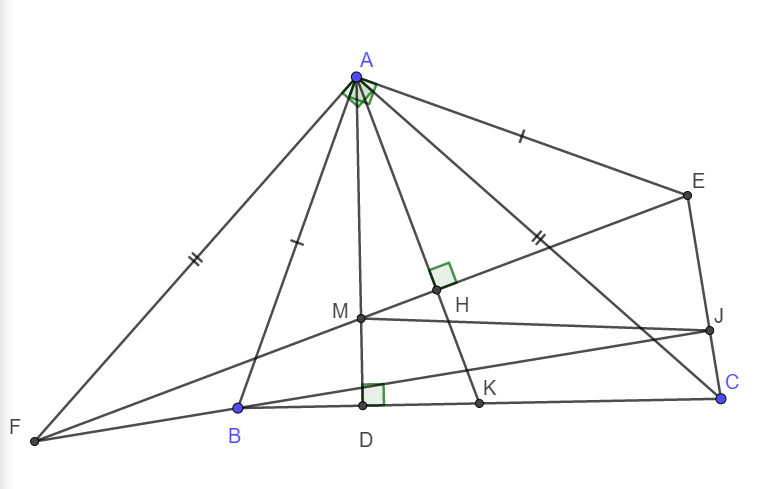
=> AN = ABsinABN = 5,93.sin38° ≈ 3,65(cm)
b) Xét tam giác ANC vuông tại N:
![]()
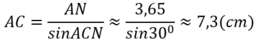

a) Xét tam giác ACK và tam giác FAM có :
AC = FA
\(\widehat{CAK}=\widehat{AFM}\) (Cùng phụ với góc \(\widehat{FAK}\) )
\(\widehat{ACK}=\widehat{FAM}\) (Cùng phụ với góc \(\widehat{DAC}\) )
\(\Rightarrow\Delta ACK=\Delta FAM\left(g-c-g\right)\)
b) Do \(\Delta ACK=\Delta FAM\left(cma\right)\Rightarrow FM=AK\)
Chứng minh hoàn toàn tương tự câu a ta có: \(\Delta ABK=\Delta EAM\left(g-c-g\right)\)
\(\Rightarrow ME=AK\)
Từ đó suy ra FM = ME hay M là trung điểm EF.
c) Kéo dài FB cắt EC tại J. Ta chứng minh \(\widehat{FJE}=90^o\)
Xét tam giác FAB và tam giác CAE có:
FA = CA
AB = AE
\(\widehat{FAB}=\widehat{CAE}\) (Cùng phụ với góc \(\widehat{BAC}\) )
\(\Rightarrow\Delta FAB=\Delta CAE\left(c-g-c\right)\)
\(\Rightarrow FB=CE\) và \(\widehat{AFB}=\widehat{ACE}\)
Xét tứ giác AFJE có:
\(\widehat{AFJ}+\widehat{FJE}+\widehat{JEA}+\widehat{EAF}=360^o\)
\(\Rightarrow\widehat{ACE}+\widehat{FJE}+\widehat{CEA}+\widehat{EAC}+90^o=360^o\)
\(\Rightarrow\widehat{FJE}+\widehat{ACE}+\widehat{CEA}+\widehat{EAC}=270^o\)
\(\Rightarrow\widehat{FJE}+180^o=270^o\)
\(\Rightarrow\widehat{FJE}=90^o\)
Vậy nên \(FB\perp EC\) (đpcm).
Bài 2:
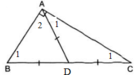
a) Gọi giao điểm của đường phân giác ^ABC và ^ACB với AC và AB lần lượt là E và D
Dễ thấy: ^BAH=^ACB (Cùng phụ với ^HAC) => 1/2. ^BAH = 1/2. ^ACB
=> ^DAM=^ACD. Mà ^DAM+^MAC=^BAC=900 => ^ACD+^MAC=900 => AM \(\perp\)CD
hay NI\(\perp\)AM.
Tương tự ta chứng minh MI\(\perp\)AN
Xét tam giác MAN: NI\(\perp\)AM; MI\(\perp\)AN => I là trực tâm của tam giác MAN (đpcm).
b) Do I là trực tâm của tam giác AMN (cmt) => AI\(\perp\)MN hay AI\(\perp\)B'C'
Ta có: Tam giác ABC có 2 đường phân giác ^ABC và ^ACB cắt nhau tại I => AI là phân giác ^BAC
=> AI là phân giác ^B'AC'.
Xét tam giác AB'C': AI là phân giác ^B'AC'. Mà AI\(\perp\)B'C' => Tam giác AB'C' cân tại A
Lại có: ^B'AC'=900 => Tam giác B'AC' vuông cân tại A.

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

a: ΔANB vuông tại N
=>tan B=AN/NB
=>AN=NB*tan38
ΔANC vuông tại N
=>AN=NC*tan30
=>NB*tan38=NC*tan30
=>NB/NC=tan30/tan38\(\simeq0,74\)
=>NB=0,74NC
mà NB+NC=11
nên \(NB\simeq4,68\left(cm\right);NC\simeq6,32\left(cm\right)\)
AN=NC*tan30=6,32*tan30\(\simeq3,65\left(cm\right)\)
b: góc BAC=180-38-30=180-68=112 độ
Xét ΔABC có BC/sinA=AC/sinB
=>\(AC=\dfrac{11}{sin112}\cdot sin38\simeq7,3\left(cm\right)\)
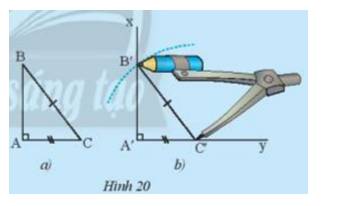

Tham khảo:
- Ta dùng êke với cạnh góc vuông đi qua đỉnh B
- Cạnh góc vuông còn lại của êke nằm trùng với AC