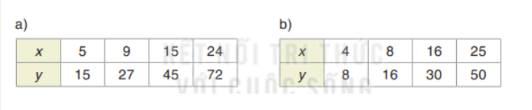
Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ thuận không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: 3.160 = 6.80 = 16.30 = 24.20 nên 2 đại lượng x, y là hai đại lượng tỉ lệ nghịch.
b) Ta có: 4.160 = 8. 80 = 320.20 \( \ne \)25.26 nên 2 đại lượng x, y không là hai đại lượng tỉ lệ nghịch.

Ta thấy: \(\dfrac{{0,5}}{{2,5}} = \dfrac{1}{5} = \dfrac{{1,5}}{{7,5}} = \dfrac{2}{{10}} = \dfrac{{2,5}}{{12,5}}\) nên x và y là 2 đại lượng tỉ lệ thuận.
Công thức liên hệ: \(x = \dfrac{1}{5}.y\) (hay y = 5.x)

Vì x và y là hai đại lượng tỉ lệ thuận theo hệ số -3 nên x = -3y
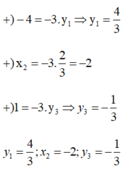
Chọn đáp án B

Vì x và y là hai đại lượng tỉ lệ thuận theo hệ số -3 nên x = -3y
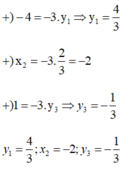
Chọn đáp án B

`\color{blue}\text {#DuyNam}`
`1,`
`a,` Vì `y` tỉ lệ thuận với `x` theo hệ số tỉ lệ `k -> y=k*x`
Thay `x=3, y=-15`
`-> -15=k*3`
`-> k=-5`
Vậy, hệ số tỉ lệ `k=-5`
`-> y=-5*x`
`b,` Khi `x=-2 -> y=-5*-2=10`
Khi `y=0,9 -> x=0,9 \div -5 = -0,18`
`2,` Hình như đề thiếu phải không bạn?
`3,`
`a,` Vì `y` tỉ lệ thuận với `x` theo hệ số tỉ lệ `7 -> y=7*x (1)`
Vì `x` tỉ lệ thuận với `z` theo hệ số tỉ lệ `0,3 -> x=0,3*z (2)`
Thay `(2)` vào `(1)`
`-> y=7*0,3*z`
`-> y=2,1*z`
`-> y` tỉ lệ thuận với `z` theo hệ số tỉ lệ `2,1`
`b,` Vì `y` tỉ lệ thuận với `x` theo hệ số tỉ lệ `a -> y=a*x (1)`
Vì `x` tỉ lệ thuận với `z` theo hệ số tỉ lệ `b -> x=b*z (2)`
Thay `(2)` vào `(1)`
`-> y=a*b*z =(a*b)*z`
`-> y` tỉ lệ thuận với `z` theo hệ số tỉ lệ `a*b`.
a) Ta có: \(\dfrac{5}{{15}} = \dfrac{9}{{27}} = \dfrac{{15}}{{45}} = \dfrac{{24}}{{72}}\) nên 2 đại lượng x, y là hai đại lượng tỉ lệ thuận.
b) Ta có: \(\dfrac{4}{8} = \dfrac{8}{{16}} = \dfrac{{25}}{{50}} \ne \dfrac{{16}}{{30}}\) nên 2 đại lượng x, y không là hai đại lượng tỉ lệ thuận.