Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

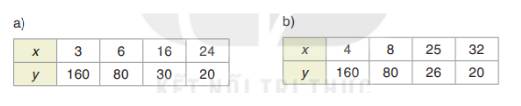
a) Ta có: 3.160 = 6.80 = 16.30 = 24.20 nên 2 đại lượng x, y là hai đại lượng tỉ lệ nghịch.
b) Ta có: 4.160 = 8. 80 = 320.20 \( \ne \)25.26 nên 2 đại lượng x, y không là hai đại lượng tỉ lệ nghịch.

Ta thấy: \(\dfrac{{0,5}}{{2,5}} = \dfrac{1}{5} = \dfrac{{1,5}}{{7,5}} = \dfrac{2}{{10}} = \dfrac{{2,5}}{{12,5}}\) nên x và y là 2 đại lượng tỉ lệ thuận.
Công thức liên hệ: \(x = \dfrac{1}{5}.y\) (hay y = 5.x)

Vì x và y là hai đại lượng tỉ lệ thuận theo hệ số -3 nên x = -3y
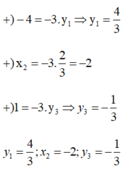
Chọn đáp án B

Vì x và y là hai đại lượng tỉ lệ thuận theo hệ số -3 nên x = -3y
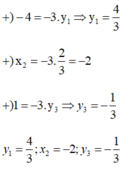
Chọn đáp án B

`\color{blue}\text {#DuyNam}`
`1,`
`a,` Vì `y` tỉ lệ thuận với `x` theo hệ số tỉ lệ `k -> y=k*x`
Thay `x=3, y=-15`
`-> -15=k*3`
`-> k=-5`
Vậy, hệ số tỉ lệ `k=-5`
`-> y=-5*x`
`b,` Khi `x=-2 -> y=-5*-2=10`
Khi `y=0,9 -> x=0,9 \div -5 = -0,18`
`2,` Hình như đề thiếu phải không bạn?
`3,`
`a,` Vì `y` tỉ lệ thuận với `x` theo hệ số tỉ lệ `7 -> y=7*x (1)`
Vì `x` tỉ lệ thuận với `z` theo hệ số tỉ lệ `0,3 -> x=0,3*z (2)`
Thay `(2)` vào `(1)`
`-> y=7*0,3*z`
`-> y=2,1*z`
`-> y` tỉ lệ thuận với `z` theo hệ số tỉ lệ `2,1`
`b,` Vì `y` tỉ lệ thuận với `x` theo hệ số tỉ lệ `a -> y=a*x (1)`
Vì `x` tỉ lệ thuận với `z` theo hệ số tỉ lệ `b -> x=b*z (2)`
Thay `(2)` vào `(1)`
`-> y=a*b*z =(a*b)*z`
`-> y` tỉ lệ thuận với `z` theo hệ số tỉ lệ `a*b`.
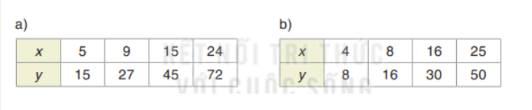
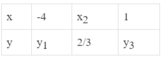
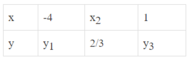
a) Ta có: \(\dfrac{5}{{15}} = \dfrac{9}{{27}} = \dfrac{{15}}{{45}} = \dfrac{{24}}{{72}}\) nên 2 đại lượng x, y là hai đại lượng tỉ lệ thuận.
b) Ta có: \(\dfrac{4}{8} = \dfrac{8}{{16}} = \dfrac{{25}}{{50}} \ne \dfrac{{16}}{{30}}\) nên 2 đại lượng x, y không là hai đại lượng tỉ lệ thuận.