Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

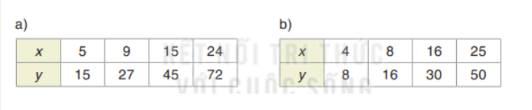
a) Ta có: \(\dfrac{5}{{15}} = \dfrac{9}{{27}} = \dfrac{{15}}{{45}} = \dfrac{{24}}{{72}}\) nên 2 đại lượng x, y là hai đại lượng tỉ lệ thuận.
b) Ta có: \(\dfrac{4}{8} = \dfrac{8}{{16}} = \dfrac{{25}}{{50}} \ne \dfrac{{16}}{{30}}\) nên 2 đại lượng x, y không là hai đại lượng tỉ lệ thuận.

Ta thấy: \(\dfrac{{0,5}}{{2,5}} = \dfrac{1}{5} = \dfrac{{1,5}}{{7,5}} = \dfrac{2}{{10}} = \dfrac{{2,5}}{{12,5}}\) nên x và y là 2 đại lượng tỉ lệ thuận.
Công thức liên hệ: \(x = \dfrac{1}{5}.y\) (hay y = 5.x)

a) Xét a.b ta có :
a.b = 1.60 = 2.30 = 3.20 = 4.15 = 5.12 vì cùng bằng 60
Vậy a tỉ lệ nghịch với b
b) Xét m.n ta có :
m.n = (-2).(-12) = (-1).(-24) = 1.24 = 2.12 ≠ 3.9
Ta thấy khi m = 3 và n = 9 thì hệ số tỉ lệ là khác với các giá trị còn lại nên m không tỉ lệ nghịch với n.

\(\text{Gọi hstl là }a\\ \Rightarrow x_1y_1=x_2y_2=a\\ \Rightarrow\dfrac{y_1}{x_2}=\dfrac{y_2}{x_1}=\dfrac{y_1}{5}=\dfrac{y_2}{6}=\dfrac{8y_1-5y_2}{40-30}=\dfrac{50}{10}=5\\ \Rightarrow\left\{{}\begin{matrix}y_1=25\\y_2=30\end{matrix}\right.\\ \Rightarrow a=x_1y_1=25\cdot6=150\)
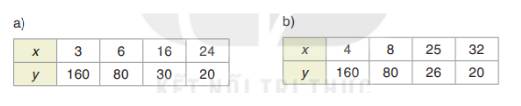

a) Ta có: 3.160 = 6.80 = 16.30 = 24.20 nên 2 đại lượng x, y là hai đại lượng tỉ lệ nghịch.
b) Ta có: 4.160 = 8. 80 = 320.20 \( \ne \)25.26 nên 2 đại lượng x, y không là hai đại lượng tỉ lệ nghịch.