Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 51, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số chia cho 17 dư 2 và chia cho 3 dư 1”.
b) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5”.


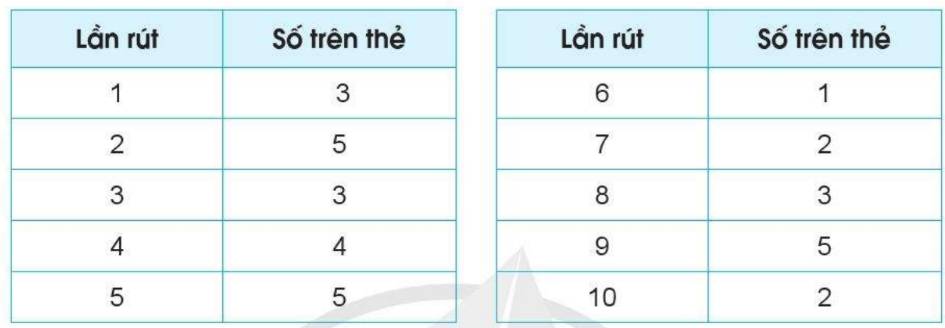

Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ rút ra là: B = {1, 2, 3, …, 51, 52}.
Số phần tử của B là 52.
a) Trong các số từ 1 đến 52 có ba số chia 17 dư 2 là: 2, 19, 36. Trong 3 số trên, có một số chia 3 dư 1 là 19.
Vậy có một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia cho 17 dư 2 và chia cho 3 dư 1” là: 19.
Vì thế, xác suất của biến cố trên là: \(\dfrac{1}{{52}}\)
b) Có tám kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5” là: 5, 15, 25, 35, 45, 50, 51, 52.
Vì thế, xác suất của biến cố trên là: \(\dfrac{8}{{52}} = \dfrac{2}{{13}}\)