Quan sát Hình 54, trong đó Cx song song với AB.
a) Tính số đo góc BCx.
b) Chứng minh rằng Cx song song với DE.
c) Tính số đo góc BCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
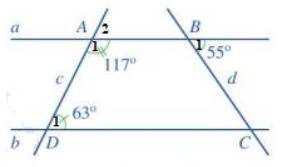
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù) nên \(117^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 117^\circ = 63^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{D_1}}\) ( cùng bằng 63 độ)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) a // b (Dấu hiệu nhận biết hai đường thẳng song song) ( đpcm)
b) Vì a // b nên \(\widehat {{B_1}} = \widehat {BCD}\) ( 2 góc so le trong), mà \(\widehat {{B_1}} = 55^\circ \Rightarrow \widehat {BCD} = 55^\circ \)
NK
8 tháng 10 2016
a, goc b= goc amn vi la 2 goc dong vi; goc c= goc anm tuong tu
b, la goc vuong vi a song song bc ma cx vuong voi bc nen cx vuong voi a
c, vi ay song song voi a ma a vuong goc voi cx nen ay vuong goc voi cx
17 tháng 12 2021
2: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
Suy ra: AD//BC
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx
b) Vì mq // xt nên \(\widehat {BAC} = \widehat {zEt}\) ( 2 góc đồng vị) nên \(\widehat {BAC} = 45^\circ \).
Vì mq // xt nên \(\widehat {CDE} = \widehat {ABC}\) ( 2 góc so le trong) nên \(\widehat {CDE} = 37^\circ \).
c)
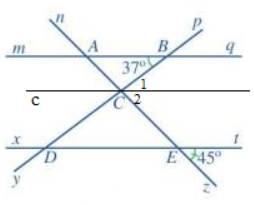
Bạn Nam nói đúng vì:
Vì c // mq nên \(\widehat {ABC} = \widehat {{C_1}}\) ( 2 góc so le trong) nên \(\widehat {{C_1}} = 37^\circ \)
Vì c // xt nên \(\widehat {CED} = \widehat {{C_2}}\) ( 2 góc so le trong) nên \(\widehat {{C_2}} = 45^\circ \)
Vì \(\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}\) nên \(\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ \)
HT
4 tháng 12 2021
Vẽ góc AOB có số đo bằng 80độ . Lấy C ∈ OA và D ∈ OB . Vẽ các tia Cx và Dy trong góc AOB sao cho ACx = 35độ ; BDy=45độ . Chứng minh Cx//dy
a) Vì Cx // AB nên \(\widehat {ABC} = \widehat {BCx}\) ( 2 góc so le trong), mà \(\widehat {ABC} = 45^\circ \Rightarrow \widehat {BCx} = 45^\circ \)
b) Vì AE \( \bot \) AB; AE \( \bot \) ED nên AB // ED (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
Mà Cx // AB (gt)
\( \Rightarrow \) Cx // ED (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)
c) Vì Cx // ED nên \(\widehat {EDC} = \widehat {DCx}\) ( 2 góc so le trong), mà \(\widehat {EDC} = 60^\circ \Rightarrow \widehat {DCx} = 60^\circ \)
Vì tia Cx nằm trong góc BCD nên \(\widehat {BCD} = \widehat {BCx} + \widehat {DCx} = 45^\circ + 60^\circ = 105^\circ \)