Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

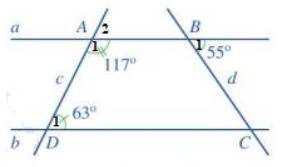
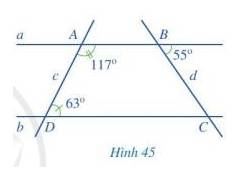
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù) nên \(117^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 117^\circ = 63^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{D_1}}\) ( cùng bằng 63 độ)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) a // b (Dấu hiệu nhận biết hai đường thẳng song song) ( đpcm)
b) Vì a // b nên \(\widehat {{B_1}} = \widehat {BCD}\) ( 2 góc so le trong), mà \(\widehat {{B_1}} = 55^\circ \Rightarrow \widehat {BCD} = 55^\circ \)

a, goc b= goc amn vi la 2 goc dong vi; goc c= goc anm tuong tu
b, la goc vuong vi a song song bc ma cx vuong voi bc nen cx vuong voi a
c, vi ay song song voi a ma a vuong goc voi cx nen ay vuong goc voi cx

2: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
Suy ra: AD//BC

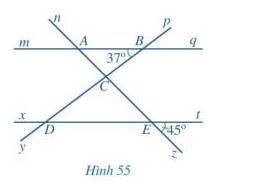
a) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx
b) Vì mq // xt nên \(\widehat {BAC} = \widehat {zEt}\) ( 2 góc đồng vị) nên \(\widehat {BAC} = 45^\circ \).
Vì mq // xt nên \(\widehat {CDE} = \widehat {ABC}\) ( 2 góc so le trong) nên \(\widehat {CDE} = 37^\circ \).
c)
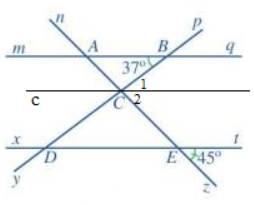
Bạn Nam nói đúng vì:
Vì c // mq nên \(\widehat {ABC} = \widehat {{C_1}}\) ( 2 góc so le trong) nên \(\widehat {{C_1}} = 37^\circ \)
Vì c // xt nên \(\widehat {CED} = \widehat {{C_2}}\) ( 2 góc so le trong) nên \(\widehat {{C_2}} = 45^\circ \)
Vì \(\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}\) nên \(\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ \)

Vẽ góc AOB có số đo bằng 80độ . Lấy C ∈ OA và D ∈ OB . Vẽ các tia Cx và Dy trong góc AOB sao cho ACx = 35độ ; BDy=45độ . Chứng minh Cx//dy

a) Vì Cx // AB nên \(\widehat {ABC} = \widehat {BCx}\) ( 2 góc so le trong), mà \(\widehat {ABC} = 45^\circ \Rightarrow \widehat {BCx} = 45^\circ \)
b) Vì AE \( \bot \) AB; AE \( \bot \) ED nên AB // ED (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
Mà Cx // AB (gt)
\( \Rightarrow \) Cx // ED (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)
c) Vì Cx // ED nên \(\widehat {EDC} = \widehat {DCx}\) ( 2 góc so le trong), mà \(\widehat {EDC} = 60^\circ \Rightarrow \widehat {DCx} = 60^\circ \)
Vì tia Cx nằm trong góc BCD nên \(\widehat {BCD} = \widehat {BCx} + \widehat {DCx} = 45^\circ + 60^\circ = 105^\circ \)