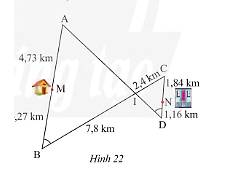
Đường đi và khoảng cách từ nhà anh Thanh (điểm \(M\)) đến công ty (điểm \(N\)) được thể hiện trong Hình 22. Hãy tìm con đường ngắn nhất để đi từ nhà anh Thanh đến công ty.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 11 2021
Ai làm nhanh tớ tick. ( Quan trọng cách trình bày nhá)
3 tháng 11 2021
1 hình tứ giác lồi có 4 đỉnh là 4 nhà máy sản xuất thép được đặt ở 4 địa điểm khác nhau tạo thành
\(\Rightarrow\) Công ty phải đặt trung tâm điều hành ở giao điểm 2 đường chéo của hình tứ giác đó
CM
16 tháng 7 2018
Đáp án B
Phân tích:
● Ta có thể mô tả bài toán trên bằng hình vẽ sau:
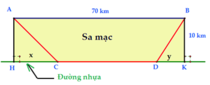
● Như đã phân tích ở trên, nếu đi trực tiếp từ A đến B trên sa mạc với vận tốc và khoảng cách hiện có thì nhà địa chất học không thể đến đúng thời gian quy định
● Vì vậy cần thiết phải chia quãng đường đi được thành 3 giai đoạn:
Giai đoạn 1: đi từ A đến C (từ sa mạc đến đường nhựa song song)
Giai đoạn 2: đi từ C đến D (một quãng đường nào đó trên đường nhựa)
Giai đoạn 3: đi từ D đến B (từ điểm kết thúc D trên đường nhựa đi tiếp đến B băng qua sa mạc).
Goi H, K, C, D là các điểm như hình vẽ.
B
24 tháng 1 2021
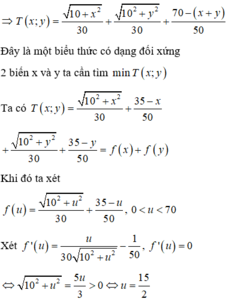
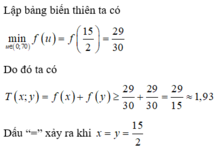
Gọi x là qđ AB
Thời gian đi từ A đến B là: x/40
Thời gian đi từ B về A là: x/30T
ổng tg hết 6h30'=13/2 (h)
=> x/40 + x/30 + 3=13/2
=> 3x/120 + 4x/120+ 360/120=780/120
=> 7x + 360=780=> 7x=420
=> x=60
vậy qđ AB dài 60 km
24 tháng 1 2021
Đổi \(6h30'=\dfrac{13}{2}h\)
Gọi x(km) là độ dài quãng đường từ nhà đến công ty(x>0)
Thời gian người đó đi từ nhà đến công ty:
\(\dfrac{x}{40}\)(h)
Thời gian người đó đi từ công ty về nhà:
\(\dfrac{x}{30}\)(h)
Vì tổng thời gian người đó đi từ công ty về nhà, đi từ nhà đến công ty và làm việc ở công ty là \(\dfrac{13}{2}h\) nên ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{30}+3=\dfrac{13}{2}\)
\(\Leftrightarrow\dfrac{3x}{120}+\dfrac{4x}{120}=\dfrac{13}{2}-3=\dfrac{13}{2}-\dfrac{6}{2}=\dfrac{7}{2}\)
\(\Leftrightarrow\dfrac{7x}{120}=\dfrac{7}{2}\)
\(\Leftrightarrow7x=\dfrac{120\cdot7}{2}=\dfrac{840}{2}=420\)
hay x=60(thỏa mãn ĐKXĐ)
Vậy: Độ dài quãng đường từ nhà đến công ty là 60km
KV
28 tháng 1
6 giờ 30 phút = 6,5 giờ
Gọi x (km) là độ dài quãng đường từ nhà đến công ty (x > 0)
Thời gian di: x/40 (h)
Thời gian về: x/30 (h)
Theo đề bài ta có phương trình:
x/40 + x/30 = 6,5 - 3
3x + 4x = 120.3,5
7x = 420
x = 420 : 7
x = 60 (nhận)
Vậy quãng đường từ nhà đến công ty dài 60 km
Ta có: \(AB = AM + MB = 4,73 + 4,27 = 9m\);\(CD = CN + ND = 1,84 + 1,16 = 3m\)
Xét tam giác \(AIB\) tam giác \(CID\) ta có:
\(\widehat {ABI} = \widehat {CDI}\) (giả thuyết)
\(\widehat {AIB} = \widehat {CID}\) (hai góc đối đỉnh)
Do đó, \(\Delta AIB\backsim\Delta CID\) (g.g)
Suy ra, \(\frac{{AB}}{{CD}} = \frac{{AI}}{{CI}} = \frac{{BI}}{{DI}} \Leftrightarrow \frac{9}{3} = \frac{{AI}}{{2,4}} = \frac{{7,8}}{{DI}}\).
Ta có:
\(\frac{9}{3} = \frac{{AI}}{{2,4}} \Rightarrow AI = \frac{{9.2,4}}{3} = 7,2m\);\(\frac{9}{3} = \frac{{7,8}}{{ID}} \Rightarrow ID = \frac{{3.7,8}}{9} = 2,6m\).
Các con đường đi từ nhà anh Thanh đến công ty là:
Con đường: \(MB \to BI \to IC \to CN\) có độ dài là:
\(MB + BI + IC + CN = 4,27 + 7,8 + 2,4 + 1,84 = 16,31km\)
Con đường: \(MB \to BI \to ID \to DN\) có độ dài là:
\(MB + BI + ID + DN = 4,27 + 7,8 + 2,6 + 1,16 = 15,83km\)
Con đường: \(MA \to AI \to ID \to DN\) có độ dài là:
\(MA + AI + ID + DN = 4,73 + 7,2 + 2,6 + 1,16 = 15,69km\)
Con đường: \(MA \to AI \to IC \to CN\) có độ dài là:
\(MA + AI + IC + CN = 4,73 + 7,2 + 2,4 + 1,84 = 16,17km\)
Vậy đi theo con đường \(MA \to AI \to ID \to DN\) là ngắn nhất.