Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tỉ số:
\(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\).
Xét tam giác\(DEF\) và tam giác\(ABC\) có:
\(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên)
Do đó, \(\Delta DEF\backsim\Delta ABC\).
Tỉ số:
\(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\).
Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau.
Tỉ số:
\(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\).
Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau.

Xét tam giác vuông \(PQR\) có:
\(\widehat P + \widehat Q + \widehat R = 180^\circ \Leftrightarrow \widehat P + 90^\circ + 42^\circ = 180^\circ \Rightarrow \widehat P = 180^\circ - 90^\circ - 42^\circ = 48^\circ \)
Xét tam giác vuông \(UVT\) có:
\(U{V^2} = U{T^2} + V{T^2} \Leftrightarrow {6^2} = U{T^2} + {4^2} \Rightarrow U{T^2} = {6^2} - {4^2} = 20 \Rightarrow UT = 2\sqrt 5 \)
Xét tam giác vuông \(DEF\) có:
\(E{F^2} = D{E^2} + D{F^2} \Leftrightarrow E{F^2} = {9^2} + {12^2} \Rightarrow E{F^2} = 225 \Rightarrow EF = 15\)
Xét tam giác vuông \(MNK\) có:
\(K{N^2} = K{M^2} + M{N^2} \Leftrightarrow {9^2} = K{M^2} + {6^2} \Rightarrow K{M^2} = {9^2} - {6^2} = 45 \Rightarrow KM = 3\sqrt 5 \)
Xét tam giác vuông \(IGH\) có:
\(I{H^2} = H{G^2} + I{G^2} \Leftrightarrow I{H^2} = 7,{5^2} + {10^2} \Rightarrow I{H^2} = 156,25 \Rightarrow IH = 12,5\)
- Xét \(\Delta ABC\) và \(\Delta QPR\) có:
\(\widehat B = \widehat P = 48^\circ \) (chứng minh trên)
\(\widehat A = \widehat Q = 90^\circ \)
Do đó, \(\Delta ABC\backsim\Delta QPR\) (g.g)
- Xét \(\Delta UTV\) và \(\Delta KMN\) có:
\(\widehat T = \widehat M = 90^\circ \)
\(\frac{{UT}}{{KM}} = \frac{{2\sqrt 5 }}{{3\sqrt 5 }} = \frac{2}{3};\frac{{VT}}{{MN}} = \frac{4}{6} = \frac{2}{3}\)
Do đó, \(\Delta UTV\backsim\Delta KMN\) (c.g.c)
- Xét \(\Delta DEF\) và \(\Delta GHI\) có:
\(\widehat D = \widehat G = 90^\circ \)
\(\frac{{HG}}{{DE}} = \frac{{7,5}}{9} = \frac{5}{6};\frac{{IG}}{{DF}} = \frac{{10}}{{12}} = \frac{5}{6}\)
Do đó, \(\Delta DEF\backsim\Delta GHI\) (c.g.c).

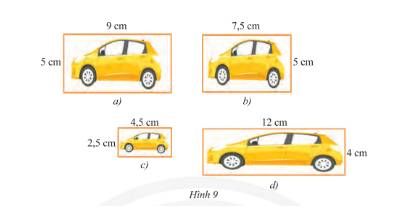
- Xét hình 9a và hình 9b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9b lần lượt là:
\(\frac{9}{{7,5}} = 1,2;\frac{5}{5} = 1\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 9b. Do đó, hình 9a và hình 9b không đồng dạng với nhau.
- Xét hình 9a và hình 9c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9c lần lượt là:
\(\frac{9}{{4,5}} = 2;\frac{5}{{2,5}} = 2\). Do đó, tồn tại hình động dạng phối cảnh của hình 9a bằng hình 9c (hình 9a thu nhỏ với tỉ số 2). Do đó, hình 9a và hình 9c đồng dạng với nhau.
- Xét hình 9a và hình 9d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9d lần lượt là:
\(\frac{9}{{12}} = 0,75;\frac{5}{4} = 1,25\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 9b. Do đó, hình 9a và hình 9b không đồng dạng với nhau.

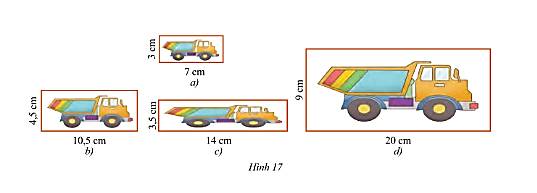
- Xét hình 17a và hình 17b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 17a và hình 17b lần lượt là:
\(\frac{7}{{10,5}} = \frac{2}{3};\frac{3}{{4,5}} = \frac{2}{3}\). Do đó, tồn tại hình động dạng phối cảnh của hình 17a bằng hình 17b. Do đó, hình 17a và hình 17b đồng dạng với nhau.
- Xét hình 17a và hình 17c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 17a và hình 17c lần lượt là:
\(\frac{7}{{14}} = \frac{1}{2};\frac{3}{{3,5}} = \frac{6}{7}\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 17a để bằng hình 17c. Do đó, hình 17a và hình 17c không đồng dạng với nhau.
- Xét hình 17a và hình 17d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 17a và hình 17d lần lượt là:
\(\frac{7}{{20}};\frac{3}{9} = \frac{1}{3}\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 17a để bằng hình 17d. Do đó, hình 17a và hình 17d không đồng dạng với nhau.

Áp dụng định lí Py-ta-go, ta có:
\(2,1^2+h^2=3,5^2\\ \Leftrightarrow h=\sqrt{3,5^2-2,1^2}=2,8m\)

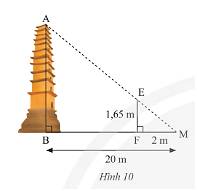
Xét \(\Delta MEF\) và \(\Delta MAB\) có:
\(\widehat M\) chung
\(\widehat {MFE} = \widehat {MBA} = 90^\circ \)
Do đó, \(\Delta MEF\backsim\Delta MAB\) (g.g)
Vì nên \(\frac{{MF}}{{MB}} = \frac{{FE}}{{AB}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{2}{{20}} = \frac{{1,65}}{{AB}} \Rightarrow AB = \frac{{1,65.20}}{2} = 16,5\)
Vậy tòa tháp cao 16,5m.

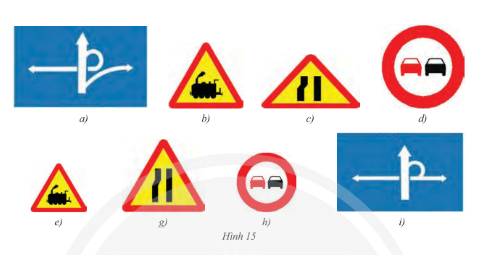
Các cặp hình đồng dạng là:
- Hình a và hình i đồng dạng với nhau;
- Hình b và hình e đồng dạng với nhau;
- Hình c và hình g đồng dạng với nhau;
- Hình d và hình h đồng dạng với nhau.

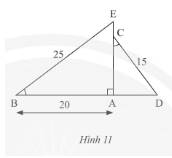
Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(\widehat {EBA} = \widehat {ACD}\) (giả thuyết)
\(\widehat {BAE} = \widehat {CAD} = 90^\circ \)
Do đó, \(\Delta ABE\backsim\Delta ACD\) (g.g)
Vì \(\Delta ABE\backsim\Delta ACD\) nên \(\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12\)cm.
Áp dụng định lí Py – ta – go cho \(\Delta ABE\) vuông tại \(A\) ta có:
\(B{E^2} = A{E^2} + A{B^2} \Leftrightarrow A{E^2} = B{E^2} - A{B^2} = {25^2} - {20^2} = 225 \Rightarrow AE = \sqrt {225} = 15\)cm.
Độ dài \(CE\) là:
15 – 12 = 3cm
Vậy \(CE = 3cm.\)
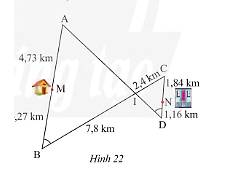





Ta có: \(AB = AM + MB = 4,73 + 4,27 = 9m\);\(CD = CN + ND = 1,84 + 1,16 = 3m\)
Xét tam giác \(AIB\) tam giác \(CID\) ta có:
\(\widehat {ABI} = \widehat {CDI}\) (giả thuyết)
\(\widehat {AIB} = \widehat {CID}\) (hai góc đối đỉnh)
Do đó, \(\Delta AIB\backsim\Delta CID\) (g.g)
Suy ra, \(\frac{{AB}}{{CD}} = \frac{{AI}}{{CI}} = \frac{{BI}}{{DI}} \Leftrightarrow \frac{9}{3} = \frac{{AI}}{{2,4}} = \frac{{7,8}}{{DI}}\).
Ta có:
\(\frac{9}{3} = \frac{{AI}}{{2,4}} \Rightarrow AI = \frac{{9.2,4}}{3} = 7,2m\);\(\frac{9}{3} = \frac{{7,8}}{{ID}} \Rightarrow ID = \frac{{3.7,8}}{9} = 2,6m\).
Các con đường đi từ nhà anh Thanh đến công ty là:
Con đường: \(MB \to BI \to IC \to CN\) có độ dài là:
\(MB + BI + IC + CN = 4,27 + 7,8 + 2,4 + 1,84 = 16,31km\)
Con đường: \(MB \to BI \to ID \to DN\) có độ dài là:
\(MB + BI + ID + DN = 4,27 + 7,8 + 2,6 + 1,16 = 15,83km\)
Con đường: \(MA \to AI \to ID \to DN\) có độ dài là:
\(MA + AI + ID + DN = 4,73 + 7,2 + 2,6 + 1,16 = 15,69km\)
Con đường: \(MA \to AI \to IC \to CN\) có độ dài là:
\(MA + AI + IC + CN = 4,73 + 7,2 + 2,4 + 1,84 = 16,17km\)
Vậy đi theo con đường \(MA \to AI \to ID \to DN\) là ngắn nhất.