cho tứ giác MNPQ có: M=700, Q=1100, P=300
1) CM: MN//PQ và tứ giác MNPQ là hình thang
2) Tính N
helpppp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho tứ giác MNPQ có: M=700, Q=1100, P=300
1) CM: MN//PQ và tứ giác MNPQ là hình thang
2) Tính N
helpppp


a: Xét ΔMNP có
H là trung điểm của MN
I là trung điểm của MP
Do đó: HI là đường trung bình
=>HI//NP và HI=NP/2(1)
Xét ΔPQN có
J là trung điểm của PQ
K là trung điểm của QN
Do đó: JK là đường trung bình
=>JK//PN và JK=PN/2(2)
Từ (1) và (2) suy ra HI//KJ và HI=KJ
hay HKJI là hình bình hành
b: Để HKJI là hình thoi thì HJ⊥KI
hay MP⊥NQ


Đáp án B
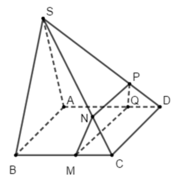
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
Đáp án B

1: Xét ΔABC có BM/BA=BN/BC=1/2
nên MN//AC và MN=1/2AC
Xét ΔADC có DP/DC=DQ/DA
nên QP//AC và QP/AC=DP/DC=1/2
=>QP=1/2AC
=>MN//PQ và MN=PQ
Xét ΔABD có AM/AB=AQ/AD=1/2
nên MQ/BD=AM/AB=1/2
=>MQ=1/2BD
Xét ΔCBD có CP/CD=CN/CB=1/2
nên NP=1/2BD
=>MQ=NP=1/2BD
mà BD=AC
nên MQ=NP=QP=MN
2: Xét tứ giác MNPQ có
MN//PQ
MN=PQ
MN=MQ
=>MNPQ là hình thoi

a) Ta có: \(MI=IN=\dfrac{MN}{2}\)(I là trung điểm của MN)
\(QK=KP=\dfrac{QP}{2}\)(K là trung điểm của QP)
mà MN=QP(Hai cạnh đối trong hình bình hành MNPQ)
nên MI=IN=QK=KP
Ta có: \(MN=2\cdot MQ\)(gt)
mà \(MN=2\cdot MI\)(I là trung điểm của MN)
nên MQ=MI
Xét tứ giác MIKQ có
MI//QK(MN//QP,I\(\in\)MN, \(K\in QP\))
MI=QK(cmt)
Do đó: MIKQ là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành MIKQ có MI=MQ(cmt)
nên MIKQ là hình thoi(Dấu hiệu nhận biết hình thoi)
b) Ta có: \(\widehat{QMN}+\widehat{AMN}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{AMN}=180^0-\widehat{QMN}=180^0-120^0\)
hay \(\widehat{AMI}=60^0\)
Ta có: MI=MQ(cmt)
mà AM=MQ(M là trung điểm của AQ)
nên AM=MI
Xét ΔMAI có AM=MI(cmt)
nên ΔMAI cân tại M(Định nghĩa tam giác cân)
Xét ΔMAI cân tại M có \(\widehat{AMI}=60^0\)(cmt)
nên ΔMAI đều(Dấu hiệu nhận biết tam giác đều)
c) Ta có: AI=AM(ΔAMI đều)
mà \(AM=MQ\)(M là trung điểm của AQ)
nên AI=MQ
mà \(MQ=\dfrac{MN}{2}\)(gt)
nên \(AI=\dfrac{MN}{2}\)
Xét ΔAMN có
AI là đường trung tuyến ứng với cạnh MN(I là trung điểm của MN)
\(AI=\dfrac{MN}{2}\)(cmt)
Do đó: ΔAMN vuông tại A(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(\widehat{NAM}=90^0\)
Ta có: AM=MQ(M là trung điểm của AQ)
mà MQ=NP(Hai cạnh đối trong hình bình hành MNPQ)
nên AM=NP
Xét tứ giác AMPN có
AM//NP(MQ//NP, A\(\in\)MQ)
AM=NP(cmt)
Do đó: AMPN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AMPN có \(\widehat{NAM}=90^0\)(cmt)
nên AMPN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)


Vì M,N lần lượt là trung điiểm của AB và AC (tgt)
=> MN // BC và MN = 1/2 BC (t/c)đường TB của tam giác)(1)
Vì P,Q l3 trung điểm của CD và BD
=> PQ//BC và PQ=1/2 BC (t/c đg Tb ...)(2)
Từ (1)và(2) => MN//PQ và MN = PQ
=> MNPQ là hbh

Bạn tự vẽ hình nha
Xét tam giác MNP có :
D là trung điểm MN ( GT )
E là trung điểm MP ( GT )
=> DE là đường trung bình của tam giác MNP
=> DE = NP/2 (1)
CMTT : DG = MQ/2 (2)
và FG = NP/2 (3)
và EF =MQ/2 (4)
Từ (1), (2), (3), (4), Mà NP = MQ ( GT )
=> DE = EF = FG= GD
Xét tứ giác DEFG có :
DE = EF = FG= GD ( CMT )
=> DEFG là hình thoi
Vậy DEFG là hình thoi
Bạn tự vẽ hình nha
Câu b)
Xét tam giác MNP có :
D là trung điểm MN ( GT )
E là trung điểm MP ( GT )
=> DE là đường trung bình của tam giác MNP
=> DE // NP
CMTT : DG // MQ
Để hình thoi DEFG là hình vuông
<=> góc GDE = 90 độ
<=> GD vuông góc DE
Ta có : DE // NP ( CMT )
và DG// MQ ( CMT )
Để GD vuông góc DE
<=> MQ vuông góc NP
Vậy tứ giác MNPQ có NP = MQ, NP vuông góc MQ thì tứ giác DEFG là hình vuông