Mn giúp tớ với. Toán 7: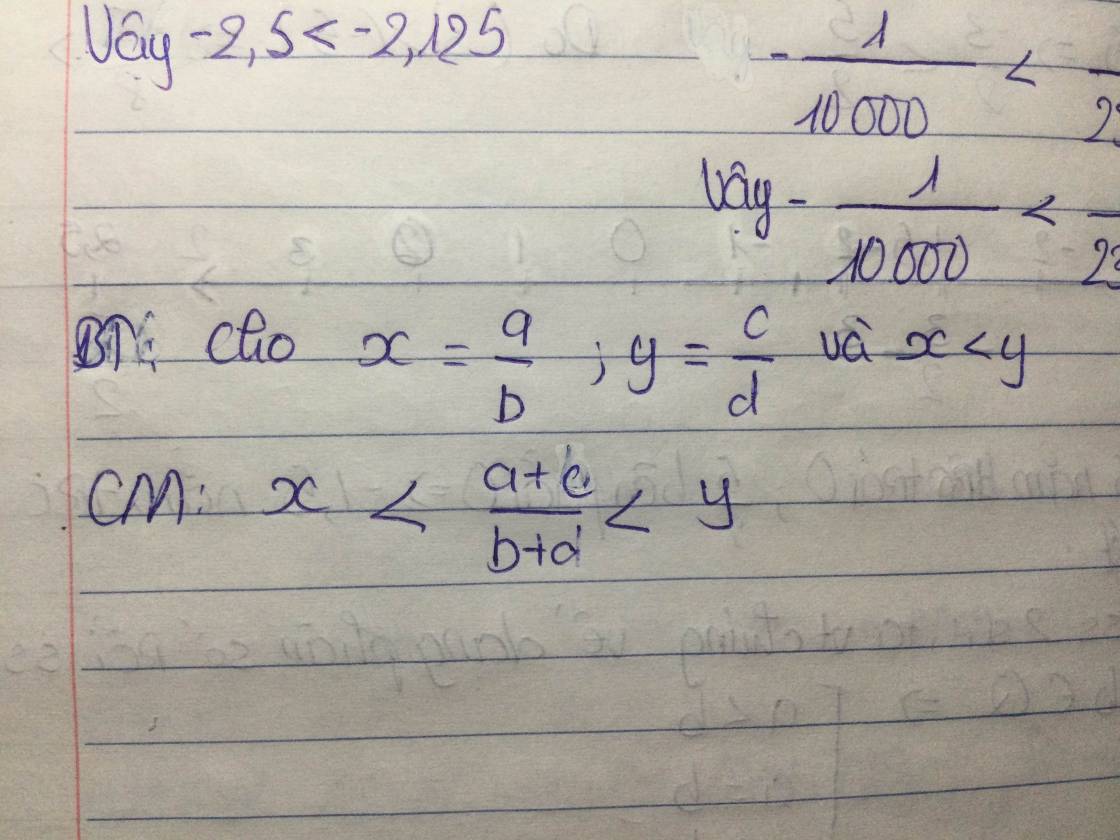 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
1
5 tháng 10 2015
Gọi x, y lần lượt là số cây trồng được của lớp 7A, 7B. Theo đề bài ta có:
x/y=0,8=8/10=4/5=>x/4=4/5 và y-x=20
Theo tính chất của dãy tỉ số bằng nhau ta có:
x/4=y/5=y-x/5-4=20/1=20
Do đó: x/4=20=>x=20.4=80
y/5=20=>y=20.5=100
Vậy số cây của lớp 7A là 80, của lớp 7B là 100
20 tháng 10 2015
a) 0,(34) = 0, (01) . 34 = \(\frac{1}{99}\). 34 = \(\frac{34}{99}\)
b) 0,(5) = 0, (1) . 5 = \(\frac{1}{9}\). 5 = \(\frac{5}{9}\)
c) 0,(123) = 0, (001) . 123 = \(\frac{1}{999}\). 123 = \(\frac{123}{999}\)= \(\frac{41}{333}\)
PT
25 tháng 5 2016
bạn tải về rồi zoom lên ý, vì đây là tớ chụp ảnh nên ảnh nhỏ
mong bạn tải về zoom lên hướng dẫn tớ với
26 tháng 10 2021
Bài 1:
a: \(x-\dfrac{3}{7}=\dfrac{2}{3}\)
\(\Leftrightarrow x=\dfrac{2}{3}+\dfrac{3}{7}=\dfrac{14+9}{21}=\dfrac{23}{21}\)
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
Sửa đề $38-12\sqrt{5}$ thành $28-12\sqrt{5}$
Lời giải:
Gọi biểu thức là $A$
Ta có:
$28-12\sqrt{5}=28-2\sqrt{180}=18-2\sqrt{18}.\sqrt{10}+10$
$=(\sqrt{18}-\sqrt{10})^2=(3\sqrt{2}-\sqrt{10})^2$
$\Rightarrow A=(3\sqrt{2}+\sqrt{10})\sqrt{(3\sqrt{2}-\sqrt{10})^2}$
$=(3\sqrt{2}+\sqrt{10})|3\sqrt{2}-\sqrt{10}|$
$=(3\sqrt{2}+\sqrt{10})(3\sqrt{2}-\sqrt{10})$
$=(3\sqrt{2})^2-(\sqrt{10})^2=18-10=8$
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 6 2023
Tổng tuổi bố và tuổi con là: 85
Tỉ số tuổi con và tuồi bố là: 1 : 4 = \(\dfrac{1}{4}\)
Ta có sơ đồ:
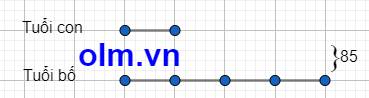
Theo sơ đồ ta có:
Tuổi con là: 85:(1 + 4) = 17 (tuổi)
Tuổi bố là: 85 - 17 = 68 (tuổi)
Hiệu số tuổi hai anh em là: 28 tuổi
Tỉ số tuổi của anh và số tuổi của em là: \(\dfrac{7}{8}\)
Ta có sơ đồ:
Theo sơ đồ ta có:
Tuổi em là: 28: (8-7)\(\times\) 7 = 196 (tuổi)
Tuổi anh là: 196 + 28 = 224 (tuổi)
Đáp số:a, bố 68 tuổi, con 17 tuổi,
b, anh 224 tuổi
em 196 tuổi
Chà xem ra hai anh em có vẻ đắc đạo thành tiên rồi hay sao mà sống thọ thế em ha
Ta có:
\(x< y\)
\(\Rightarrow\dfrac{a}{b}< \dfrac{c}{d}\)
\(\Rightarrow ad< cb\)
Cộng 2 vế cho ab
\(\Rightarrow ad+ab< cb+ab\)
\(\Rightarrow a\left(b+d\right)< b\left(a+c\right)\)
\(\Rightarrow\dfrac{a}{b}< \dfrac{a+c}{b+d}\)
\(\Rightarrow x< \dfrac{a+b}{b+d}\left(1\right)\)
\(y>x\)
\(\Rightarrow\dfrac{c}{d}>\dfrac{a}{b}\)
\(\Rightarrow cb>ad\)
Cộng 2 vế cho cd:
\(\Rightarrow cb+cd>ad+cd\)
\(\Rightarrow c\left(b+d\right)>d\left(a+c\right)\)
\(\Rightarrow\dfrac{c}{d}>\dfrac{a+c}{b+d}\)
\(\Rightarrow y>\dfrac{a+b}{b+d}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow x< \dfrac{a+c}{b+d}< y\left(dpcm\right)\)