Xét tính tăng giảm của dãy số: un = \(\dfrac{3^n-1}{2^n}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{u_n}{u_{n-1}}=\dfrac{3^n}{2^{n+1}}:\dfrac{3^{n-1}}{2^n}\)
\(=\dfrac{3^n}{3^{n-1}}\cdot\dfrac{2^n}{2^{n+1}}=\dfrac{3}{2}>1\)
=>(un) là dãy tăng
c: ĐKXĐ: n>=1
\(u_n=\sqrt{n}-\sqrt{n-1}\)
\(=\dfrac{1}{\sqrt{n}+\sqrt{n-1}}\)
\(\dfrac{u_n}{u_{n-1}}=\dfrac{1}{\sqrt{n}+\sqrt{n-1}}:\dfrac{1}{\sqrt{n-1}+\sqrt{n-2}}\)
\(=\dfrac{\sqrt{n-1}+\sqrt{n-2}}{\sqrt{n-1}+\sqrt{n}}< 1\)
=>Đây là dãy số giảm


\(u_n=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{n\left(n+1\right)}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(=1-\dfrac{1}{n+1}< 1\)
=>Hàm số bị chặn trên tại \(u_n=1\)
\(n+1>=1\)
=>\(\dfrac{1}{n+1}< =1\)
=>\(-\dfrac{1}{n+1}>=-1\)
=>\(1-\dfrac{1}{n+1}>=-1+1=0\)
=>Hàm số bị chặn dưới tại 0
\(u_n=1-\dfrac{1}{n+1}=\dfrac{n+1-1}{n+1}=\dfrac{n}{n+1}\)
\(\dfrac{u_n}{u_{n+1}}=\dfrac{n}{n+1}:\dfrac{n+1}{n+2}=\dfrac{n^2+2n}{n^2+2n+1}< 1\)
=>(un) là dãy số tăng

1:
a: \(u_2=2\cdot1+3=5;u_3=2\cdot5+3=13;u_4=2\cdot13+3=29;\)
\(u_5=2\cdot29+3=61\)
b: \(u_2=u_1+2^2\)
\(u_3=u_2+2^3\)
\(u_4=u_3+2^4\)
\(u_5=u_4+2^5\)
Do đó: \(u_n=u_{n-1}+2^n\)

Ta có u n = n − 1 n + 1 = 1 − 2 n + 1
Xét hiệu u n + 1 − u n = 1 − 2 n + 2 − 1 − 2 n + 1
= 2 n + 1 − 2 n + 2 = 2 ( n + 2 ) − 2 ( n + 1 ) ( n + 1 ) . ( n + 2 ) = 2 ( n + 1 ) ( n + 2 ) > 0 ∀ n ∈ ℕ *
Kết luận dãy số ( u n ) là dãy số tăng.
Chọn đáp án D.

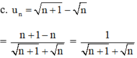
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
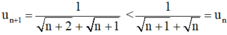
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
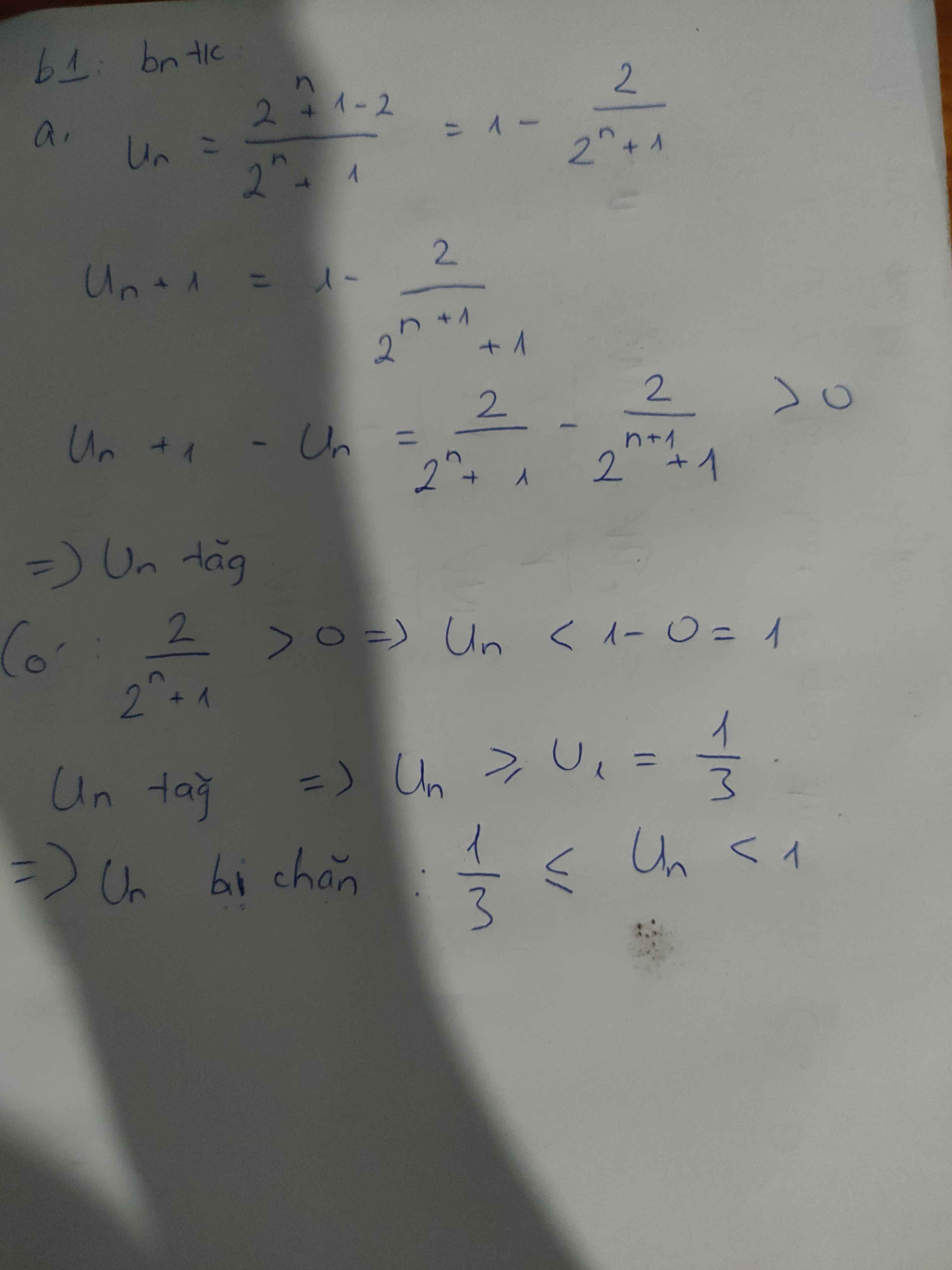
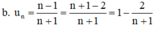
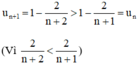
\(u_n=\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}=\dfrac{3^{n+1}-1}{2^{n+1}}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{3^{n+1}-1}{2^{n+1}}-\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{2^n.3^{n+1}-2^n-2^{n+1}.3^n+2^{n+1}}{2^n.2^{n+1}}\)
\(=\dfrac{2^n.3^n\left(3-2\right)-2^n\left(2-1\right)}{2^{2n+1}}\)
\(=\dfrac{2^n.\left(3^n-1\right)}{2^{2n+1}}\)
\(=\dfrac{\left(3^n-1\right)}{2}>0\left(n>1\right)\)
Vậy dãy \(u_n\)đã cho tăng