1) cho dãy \(\left(u_n\right)\) xác định bởi \(u_n=2.3^n\) giá trị của \(u_{20}\) với mọi số nguyên dương là
A. 2.\(3^{19}\) B.\(2.3^{20}\) C.\(3^{20}\) D.\(2.3^{21}\)
2) cho dãy \(\left(u_n\right)\) xác định bởi \(u_n=3^n\) số hạng \(u_{n+1}\) là
A. \(3^n+1\) B.\(3^n+3\) C.\(3^n.3\) D.\(3\left(n+1\right)\)
3) cho dãy số \(\left(u_n\right)\) với \(u_n=4^n+2^n\) ba số hạng đầu tiên của dãy là
4) cho dãy số \(\left(u_n\right)\) n ϵ N* biết \(u_n=\dfrac{1}{n+1}\) ba số hạng đầu tiên của dãy số đó là
5) cho dãy số có các số hạng đầu tiên là 5,10,15,20,25,.. số hạng tổng quát của dãy số là

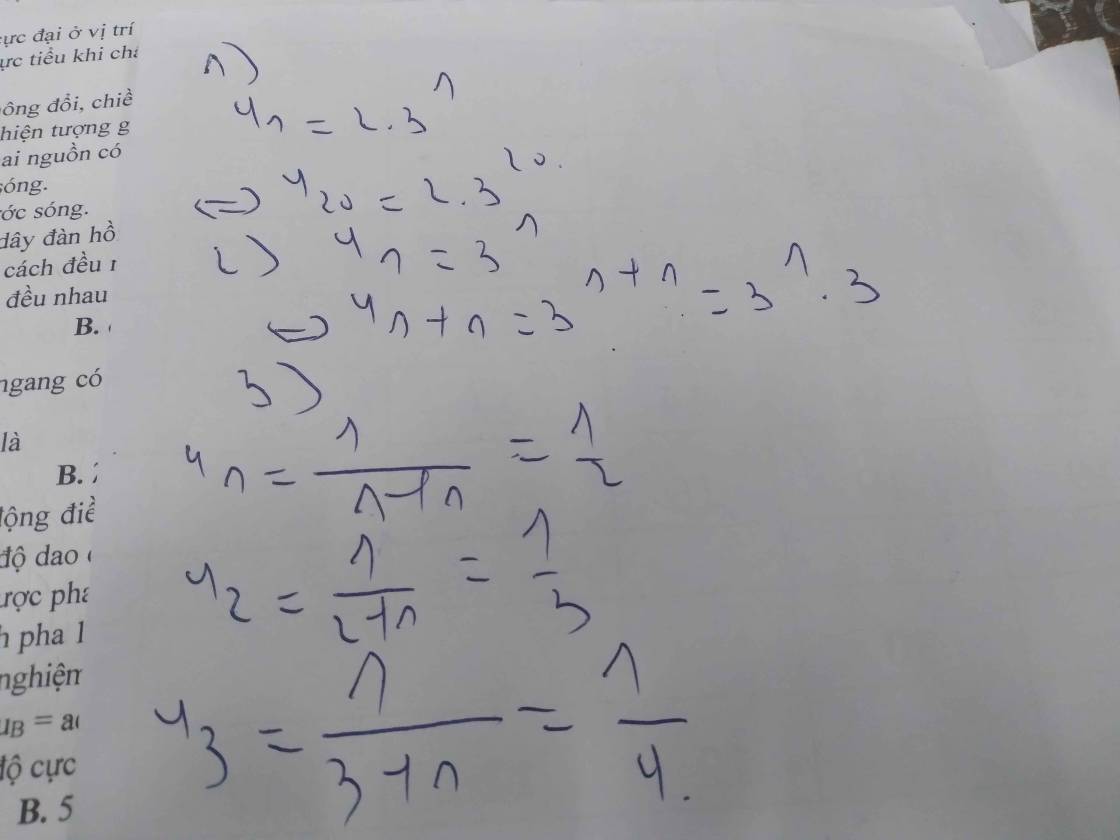
5: \(u_n=5n\left(n\in N\right)\)
4: Ba số hạng đầu tiên là 1/2;1/3;1/4
3: Ba số hạng đầu tiên là 6;20;72
2C
1B