
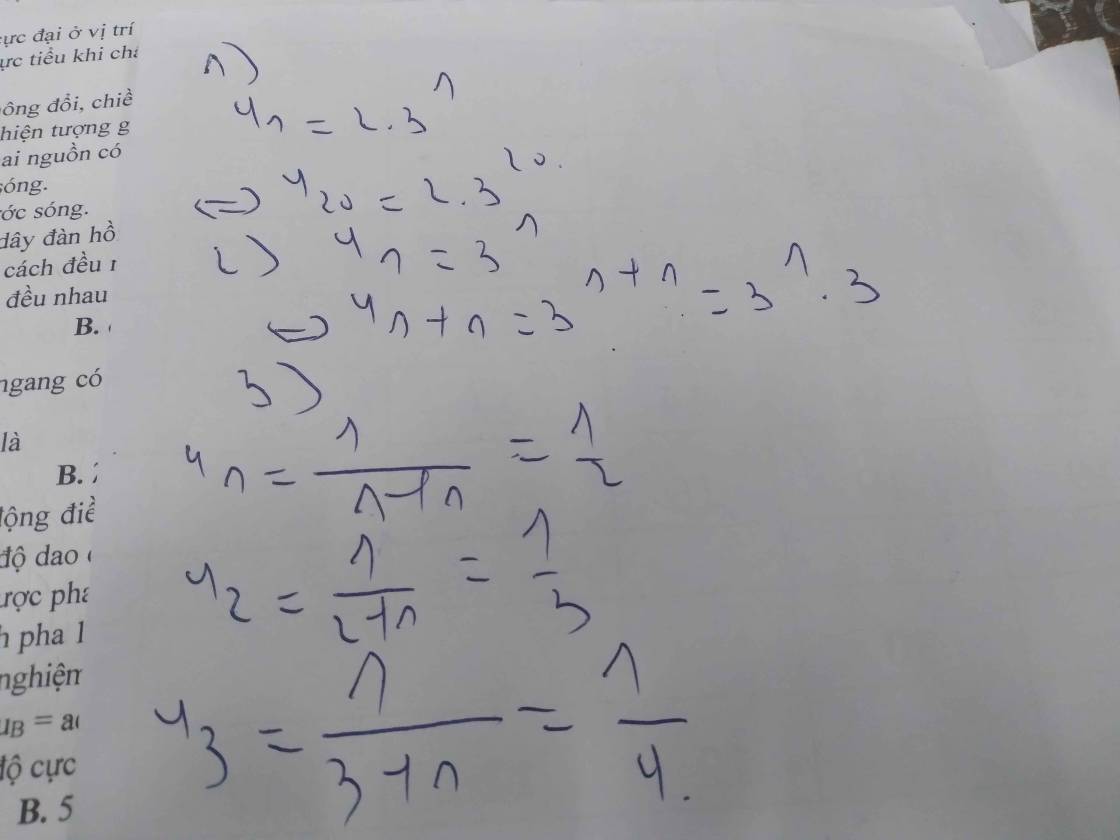
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

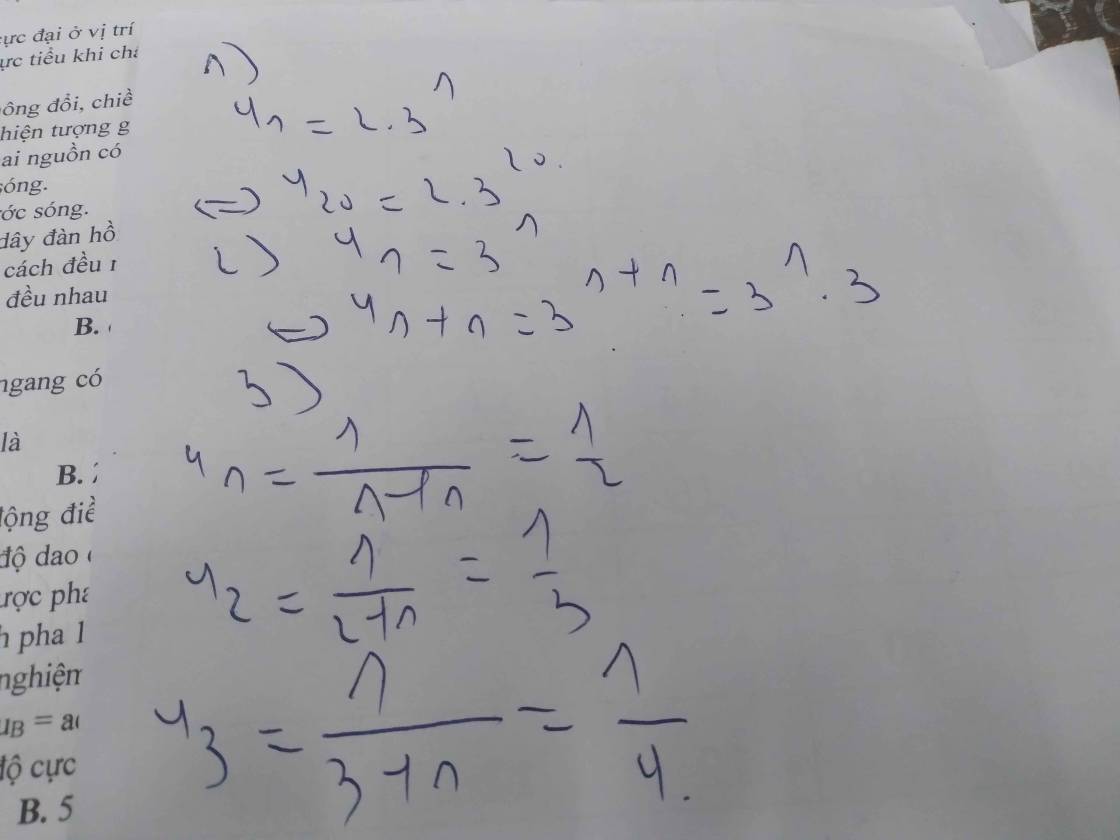

a) Ta có:
u1 = 2, u2 = 2u1 – 1 = 3, u3 = 2u2 – 1= 5
u4 = 2u3 -1 = 9, u5 = 2u4 – 1= 10
b) Với n = 1, ta có: u1 = 21-1 + 1 = 2 : đúng
Giả sử công thức đúng với n = k. Nghĩa là: uk = 2k-1 + 1
Ta chứng minh công thức cũng đúng với n = k + 1,
Nghĩa là chứng minh:
Uk+1 = 2(k+1)-1 + 1 = 2k + 1
Ta có: uk+ 1 = 2uk – 1 = 2(2k -1+ 1) -1 = 2.2k -1 + 2 – 1 = 2k + 1 (đpcm)
Vậy un = 2n-1 + 1 với mọi n ∈ N*

a)
\(u_1=5\)
\(u_2-u_1=1\)
\(u_3-u_2=4\)
............
\(u_n-u_{n-1}=3\left(n-1\right)-2=3n-5\)
Cộng từng vế của đẳng thức và rút gọn ta được:
\(u_n=5+1+4+7+...+3n-5\)
\(=5+\dfrac{\left(3n-5+1\right)\left(n-1\right)}{2}=5+\dfrac{\left(3n-4\right)\left(n-1\right)}{2}\).
Vậy \(u_n=5+\dfrac{\left(3n-4\right)\left(n-1\right)}{2}\) với \(n\ge1\).
Xét hiệu:
\(u_1=5\)
\(u_n-u_{n-1}=3n-5\) \(\left(n\ge2\right)\)
Với \(n\ge2\) thì \(3n-5>0\) nên \(u_n>u_{n-1}\).
Vậy \(\left(u_n\right)\) là dãy số tăng.

TenAnh1 TenAnh1 A = (-4.36, -5.2) A = (-4.36, -5.2) A = (-4.36, -5.2) B = (11, -5.2) B = (11, -5.2) B = (11, -5.2)

a) Năm số hạng đầu của dãy số là -1, 2, 5, 8, 11.
b) Chứng minh un = 3n - 4 bằng phương pháp quy nạp:
Với n =1 thì u1 3.1 - 4 = -1, đúng.
Giả sử hệ thức đúng với n = k ≥ 1, tức là uk = 3k -4. Ta chứng minh hệ thức cũng đúng với n = k + 1.
Thật vậy, theo công thức của dãy số và giả thiết quy nạp, ta có:
uk+1 = uk + 3 = 3k - 4 + 3 = 3(k + 1) - 4.
Vậy hệ thức đúng với mọi n ε N*